Question

7．已知在△ABC中，∠C=90°，M是边BC的中点，AC=1．若sinB=$\frac{1}{3}$，则AM=$\sqrt{3}$．

Answer 1

分析 由已知sinB=$\frac{1}{3}$，可求AB，利用勾股定理可求BC的值，进而可求MC，利用勾股定理即可解得AM的值．

解答 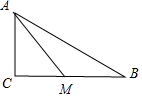解：∵∠C=90°，AC=1．sinB=$\frac{1}{3}$=$\frac{AC}{AB}$=$\frac{1}{AB}$，
∴AB=3，
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$，
∵M是边BC的中点，
∴MC=$\sqrt{2}$，
∴AM=$\sqrt{A{C}^{2}+C{M}^{2}}$=$\sqrt{{1}^{2}+（\sqrt{2}）^{2}}$=$\sqrt{3}$．
故答案为：$\sqrt{3}$．

点评 本题主要考查了勾股定理，三角函数的定义在解三角形中的应用，考查了数形结合思想和转化思想，属于基础题．