|
|
|
某工厂经奥组委授权生产销售伦敦奥运会吉祥物(精灵”文洛克”)饰品，生产该饰品的固定成本是1200(单位：万元)，生产成本c(单位：万元)与生产的饰品件数x(单位：万件)的立方成正比；该饰品单价p(单位：元)的平方与生产的饰品件数x(单位：万件)成反比，现已知生产该饰品100万件时，其单价p＝50元，生产成本c＝ ×104万元．且工厂生产的饰品都可以销售完．设工厂生产该饰品的利润为f(x)(万元)(注：利润＝销售额－固定成本－生产成本)
(Ⅰ)求函数y＝f(x)的表达式．
(Ⅱ)当生产该饰品的件数x(万件)为多少时，工厂生产该饰品的利润最大．
|
|
|
练习册系列答案
相关习题
科目：高中数学
来源：人民教育出版社（实验修订本） 高中数学
题型：
|
|
|
椭圆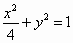 的焦点为F1，F2，点P在椭圆上，且线段PF1的中点恰好在y轴上，|PF1|＝λ|PF2|，则λ＝________．
|
|
|
查看答案和解析>>
科目：高中数学
来源：人教B版（新课标） 必修3
题型：
|
|
|
某社区有5000户家庭，其中高收入家庭1250户，中等收入家庭2800户，低收入家庭950户，为了调查社会消费力的指标，采用分层抽样的方法从中抽取1个容量若干的样本，若高收入家庭抽取了125户，则低收入家庭被抽取的户数为
|
| [ ] |
A． |
500
|
B． |
280
|
C． |
125
|
D． |
95
|
|
|
查看答案和解析>>
科目：高中数学
来源：人教B版（新课标） 选修1-1
题型：
|
|
|
若椭圆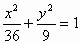 的一条弦被点(4，2)平分，则这条弦所在的直线方是________．
|
|
|
查看答案和解析>>
科目：高中数学
来源：苏教版（新课标） 必修3
题型：
|
|
|
如果某地的财政收入x与支出y满足线性回归方程y＝bx＋a＋e(单位：亿元)，其中b＝0.8，a＝2，|e|≤0.5，如果今年该地区财政收入10亿元，则年支出预计不会超过
|
| [ ] |
A． |
9亿
|
B． |
10亿
|
C． |
9.5亿
|
D． |
10.5亿
|
|
|
查看答案和解析>>
科目：高中数学
来源：苏教版（新课标） 选修2-2
题型：
|
|
|
由直线y＝－x和曲线y＝x3－4x2＋4x－2围成的图形的面积为
|
| [ ] |
A． |
|
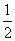
B． |
|
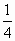
C． |
|
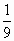
D． |
|
|
|
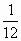
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
以平面直角坐标系的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位，已知直线的参数方程是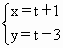 ，(t为参数)，圆C的极坐标方程是ρ＝4cos 则直线被圆C截得的弦长
|
| [ ] |
A． |
|
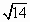
B． |
2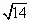
|
C． |
|
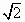
D． |
2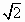
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
已知复数 z＝(5－2i)2(i为虚数单位)，则z的实部为________．
|
|
|
查看答案和解析>>
，0)，Q(2
，0)，动点N(x，y)，直线NP，NQ的斜率分别为k1，k2，且
(其中“
”可以是四则运算加、减、乘、除中的任意一种运算)，坐标原点为O，点M(2，1)．
”表示乘法，动点N的轨迹再加上P，Q两点记为曲线C，直线l平行于直线OM，且与曲线C交于A，B两个不同的点．求ΔAOB的面积S的取值范围．