
在平面直角坐标系中,以原点为极点,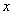 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线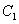 的方程为
的方程为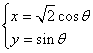 (
(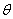 为参数),曲线
为参数),曲线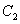 的极坐标方程为
的极坐标方程为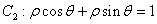 ,若曲线
,若曲线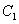 与
与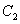 相交于
相交于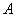 、
、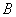 两点.
两点.
(1)求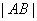 的值; (2)求点
的值; (2)求点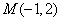 到
到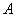 、
、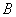 两点的距离之积.
两点的距离之积.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10···,第n个三角形数为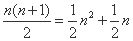 。记第n个k边形数为N(n,k)(
。记第n个k边形数为N(n,k)(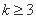 ),以下列出了部分k边形数中第n个数的表达式:
),以下列出了部分k边形数中第n个数的表达式:
三角形数 N(n,3)=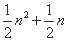 正方形数 N(n,4)=
正方形数 N(n,4)=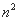
五边形数 N(n,5)=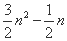 六边形数 N(n,6)=
六边形数 N(n,6)=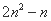
可以推测N(n,k)的表达式,由此计算N(10,24)= ____________
查看答案和解析>>
科目:高中数学 来源: 题型:
定义域为R的函数 满足
满足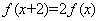 ,当
,当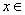 [0,2)时,
[0,2)时,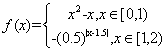 若
若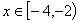 时,
时,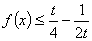 有解,则实数t的取值范围是
有解,则实数t的取值范围是
A.[-2,0)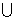 (0,l) B.[-2,0)
(0,l) B.[-2,0) 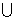 [l,+∞) C.[-2,l] D.(
[l,+∞) C.[-2,l] D.(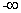 ,-2]
,-2]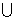 (0,l]
(0,l]
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)= 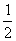
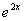 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性;
(2)若a=1,函数g(x)=(x-m)f(x)-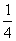
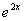 +x2+x在区间(0,+
+x2+x在区间(0,+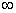 )上为增函数,求整数m 的最大值.
)上为增函数,求整数m 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
由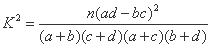 算得,
算得,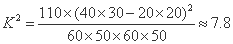
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
参照附表,得到的正确结论是:
A有99%以上的把握认为“爱好该项运动与性别有关”
B有99%以上的把握认为“爱好该项运动与性别无关”
C在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
哈三中高二某班为了对即将上市的班刊进行合理定价,将对班刊按事先拟定的价格进行试销,得到如下数据:
| 单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(I)求回归直线方程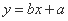 ;(其中
;(其中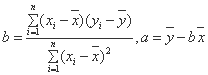 )
)
(II)预计今后的销售中,销量与单价服从(I)中的关系,且班刊的成本是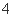 元/件,为了获得最大利润,班刊的单价定为多少元?
元/件,为了获得最大利润,班刊的单价定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com