
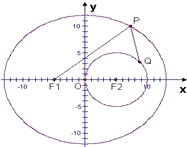
 已知点P是椭圆
已知点P是椭圆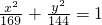 上一动点,点F1,F2是椭圆的左右两焦点.
上一动点,点F1,F2是椭圆的左右两焦点.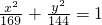
 …(4分)
…(4分) p=
p=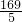 ,p=
,p= =67.6
=67.6 )
) r2r1sin30°=144(2-
r2r1sin30°=144(2- )…(13分)
)…(13分)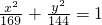 的标准方程得出a=13,b=12,c=5,从而得到长轴长26,右准线方x=
的标准方程得出a=13,b=12,c=5,从而得到长轴长26,右准线方x=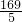 ;
; p=
p=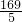 ,p=
,p= =135.2,最后写出抛物线标准方程;
=135.2,最后写出抛物线标准方程; ),根据面积公式即可求得△PF1F2的面积;
),根据面积公式即可求得△PF1F2的面积;

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
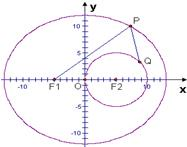 已知点P是椭圆
已知点P是椭圆| x2 |
| 169 |
| y2 |
| 144 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| MA |
| MB |
| AB |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市主城八区高三第二次调研数学试卷(理科)(解析版) 题型:解答题
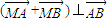 的实数m的取值范围.
的实数m的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com