
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,当
,当![]() 时,求
时,求![]() 的最大值.
的最大值.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在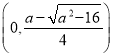 ,
,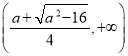 上单调递增;在
上单调递增;在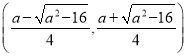 上单调递减;
上单调递减;
(2)![]()
【解析】
(1)先对函数![]() 求导,分别讨论
求导,分别讨论![]() 和
和![]() ,即可得出结果;
,即可得出结果;
(2)先由(1)得到![]() ,
,![]() ,对
,对![]() 化简整理,再令
化简整理,再令![]() ,得到
,得到![]() ,根据(1)和
,根据(1)和![]() 求出
求出![]() 的范围,再令
的范围,再令![]() ,用导数的方法求其最大值,即可得出结果.
,用导数的方法求其最大值,即可得出结果.
(1)由![]() 得
得![]() ;
;
因为![]() ,所以
,所以![]() ;
;
因此,当![]() 时,
时,![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() 得
得![]() ,解得
,解得![]() 或
或![]() ;由
;由![]() 得
得![]() ;
;
所以![]() 在
在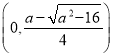 ,
,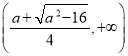 上单调递增;在
上单调递增;在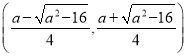 上单调递减;
上单调递减;
综上,当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在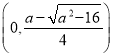 ,
,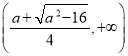 上单调递增;在
上单调递增;在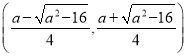 上单调递减;
上单调递减;
(2)若![]() 有两个极值点
有两个极值点![]() ,
,
由(1)可得, ![]() 是方程
是方程![]() 的两不等实根,
的两不等实根,
所以![]() ,
,![]() ,
,
因此![]()
![]() ,
,
令![]() ,则
,则![]() ;
;
由(1)可知![]() ,
,
当![]() 时,
时,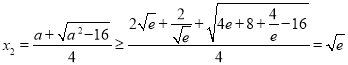 ,
,
所以![]() ,
,
令![]() ,
,![]() ,
,
则![]() 在
在![]() 上恒成立;
上恒成立;
所以![]() 在
在![]() 上单调递减,
上单调递减,
故![]() .
.
即![]() 的最大值为
的最大值为![]() .
.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占50%,苹果销量约占20%,三星销量约占30%).根据该图,以下结论中一定正确的是( )
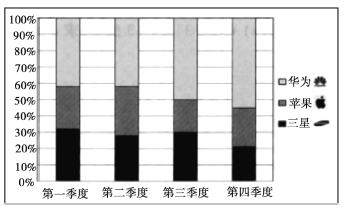
A.华为的全年销量最大B.苹果第二季度的销量大于第三季度的销量
C.华为销量最大的是第四季度D.三星销量最小的是第四季度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() 且右焦点
且右焦点![]() 到右准线
到右准线![]() 的距离为
的距离为![]() .
.
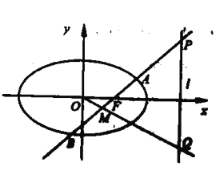
(1)求椭圆![]() 的标准方程:
的标准方程:
(2)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,与
两点,与![]() 交于点
交于点![]() 是弦
是弦![]() 的中点,直线
的中点,直线![]() 与
与![]() 交于点
交于点![]() .若
.若![]() 与
与![]() 的面积之比是
的面积之比是![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2acoskπlnx(k∈N*,a∈R且a>0).
(1)讨论函数f(x)的单调性;
(2)若k=2018,关于x的方程f(x)=2ax有唯一解,求a的值;
(3)当k=2019时,证明:对一切x∈(0,+∞),都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时期数学家、天文学家——祖暅,提出了著名的祖暅原理:“幂势既同,则积不容异也”.“幂”是截面积,“势”是几何体的高,意思是两等高几何体,若在每一等高处的两截面面积都相等,则两几何体体积相等.已知某不规则几何体与如图三视图所对应的几何体满足祖暅原理,则该不规则几何体的体积为( )
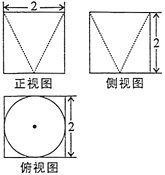
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】普通高中国家助学金,用于资助家庭困难的在校高中生.在本地,助学金分一等和二等两类,一等助学金每学期1250元,二等助学金每学期750元,并规定:属于农村建档立卡户的学生评一等助学金.某班有10名获得助学金的贫困学生,其中有3名属于农村建档立卡户,这10名学生中有4名获一等助学金,另6名获二等助学金.现从这10名学生中任选3名参加座谈会.
(Ⅰ)若事件A表示“选出的3名同学既有建档立卡户学生,又有非建档立卡户学生”,求A的概率;
(Ⅱ)设X为选出的3名同学一学期获助学金的总金额,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
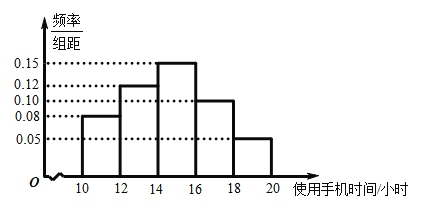
【题目】为了解学生课外使用手机的情况,某研究学习小组为研究学校学生一个月使用手机的总时间,收集了500名学生2019年12月课余使用手机的总时间(单位:小时)的数据.从中随机抽取了50名学生,将数据进行整理,得到如图所示的频率分布直方图.已知这50人中,恰有2名女生的课余使用手机总时间在![]() 区间,现在从课余使用手总时间在
区间,现在从课余使用手总时间在![]() 样本对应的学生中随机抽取2人,则至少抽到1名女生的概率为( )
样本对应的学生中随机抽取2人,则至少抽到1名女生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com