练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    圆C1：x2+y2+4x-4y+4=0与圆C2：x2+y2-4x-10y+13=0的公切线有（　　）
    A、1条B、2条C、3条D、4条
    考点：两圆的公切线条数及方程的确定
    专题：直线与圆
    分析：分别求出两圆的半径和圆心距，由此得到两圆相交，从而能求出两公切线的条数．
    解答：解：∵圆C1：x2+y2+4x-4y+4=0的圆心C1（-2，2），半径r1 =
    1
    2
    		16+16-16
    =2，
    圆C2：x2+y2-4x-10y+13=0的圆心C2（2，5），半径r2=
    1
    2
    		16+100-52
    =4，
    |C1C2|=
    		(2+2)2+(5-2)2
    =5，
    ∵|r1-r2|＜|C1C2|＜r1+r2，
    ∴圆C1：x2+y2+4x-4y+4=0与圆C2：x2+y2-4x-10y+13=0相交，
    ∴圆C1：x2+y2+4x-4y+4=0与圆C2：x2+y2-4x-10y+13=0的公切线有2条．
    故选：B．
    点评：本题考查两圆的公切线的条数的求法，是基础题，解题时要注意两圆位置关系的合理运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知正六边形的半径为6cm，求它的外接圆和内切圆所围成的圆环面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

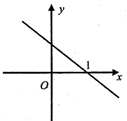    函数f（x）的导函数f′（x）的图象是如图所示的一条直线l，l与x轴交点的坐标为（1，0），则f（0）和f（3）的大小关系为（　　）
    A、f（0）＜f（3）
    B、f（0）＞f（3）
    C、f（0）=f（3）
    D、不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    用半径为R的圆形铁皮剪出一个圆心角为α的扇形，制成一个圆锥形容器，要使容器的容积最大，扇形的圆心角α=（　　）
    A、
    2π
    3
    B、
    2
    		3
    3
    π
    C、
    		6
    3
    π
    D、
    2
    		6
    3
    π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在矩形OABC内：记曲线y=x3与直线y=x围成的区域为M（图中阴影部分）．随机往矩形OABC内投一点P，则点P落在区域M内的概率是（　　）
    A、
    1
    18
    B、
    7
    32
    C、
    5
    32
    D、
    1
    16

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C1：x2+y2=1，圆C2：x2+y2-8x-6y+21=0则两圆公切线的条数有（　　）
    A、1条B、2条C、3条D、4条

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    圆x2+y2=1和4x2+4y2-16x-8y+11=0的公切线的斜率是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知cos（α-
    π
    6
    ）+sinα=
    4
    5
    		3
    ，则sin（α+
    π
    6
    ）的值是（　　）
    A、
    4
    5
    B、-
    4
    5
    C、
    4
    		3
    15
    D、-
    4
    		3
    15

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法正确的是（　　）
    A、我校爱好足球的同学组成一个集合
    B、{1，2，3}是不大于3的自然数组成的集合
    C、集合{1，2，3，4，5}和{5，4，3，2，1}表示同一集合
    D、数1，0，5，
    1
    2
    ，
    3
    2
    ，
    6
    4
    ，
    1
    4
    组成的集合有7个元素

    查看答案和解析>>

    同步练习册答案