
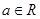 且
且 ,设函数
,设函数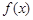 = ax2 +x-3alnx.
= ax2 +x-3alnx.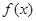 的单调区间;
的单调区间;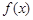 ≤2x-2.
≤2x-2.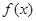 的单调递增区间为(0,
的单调递增区间为(0,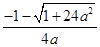 )、递减区间为(
)、递减区间为(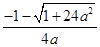 ,
,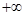 ); (II)见解析。
); (II)见解析。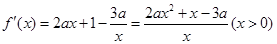 ,然后再根据导数大于(小于)零,分别求出其单调增(减)区间.
,然后再根据导数大于(小于)零,分别求出其单调增(减)区间.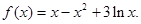 ,然后构造函数
,然后构造函数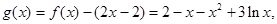 再利用导数求g(x)的最大值,证明其最大值不大于零即可.
再利用导数求g(x)的最大值,证明其最大值不大于零即可.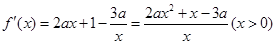 …………………………1分
…………………………1分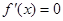 解得
解得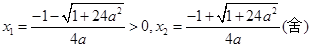 …………………3分
…………………3分| x | (0,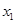 ) ) | | (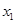 , ,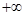 ) ) |
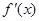 | + | | - |
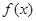 |  | |  |
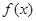 的单调递增区间为(0,
的单调递增区间为(0,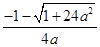 )、递减区间为(
)、递减区间为(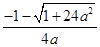 ,
,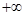 )…………………7分
)…………………7分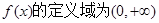 ,a=-1时,
,a=-1时,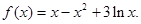
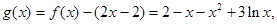 ………………………………9分
………………………………9分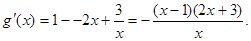 ……………………10分
……………………10分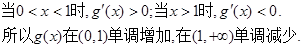 ……………………12分
……………………12分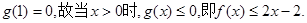 ……………………14分
……………………14分

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源:不详 题型:解答题
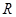 的单调函数
的单调函数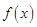 是奇函数,当
是奇函数,当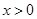 时,
时,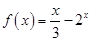 .
.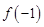 的值;
的值;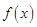 的解析式;
的解析式;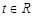 ,不等式
,不等式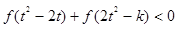 恒成立,求实数
恒成立,求实数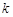 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
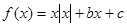 ,给出以下四个命题:①当c=0时,有
,给出以下四个命题:①当c=0时,有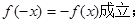 ②当b=0,c>0时,方程
②当b=0,c>0时,方程 ③函数
③函数 的图象关于点(0,c)对称 ④当x>0时;函数
的图象关于点(0,c)对称 ④当x>0时;函数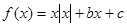 ,
, 。其中正确的命题的序号是_________。
。其中正确的命题的序号是_________。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
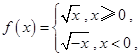 且
且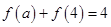 ,那么
,那么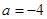 ;
;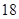 ,
,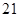 ,
,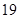 ,
,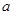 ,
,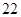 的平均数是
的平均数是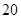 ,那么这组数据的方差是
,那么这组数据的方差是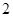 ;
; 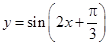 的图象,只要将
的图象,只要将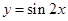 的图象向左平移
的图象向左平移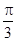 单位;
单位;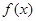 在
在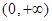 为增函数,且
为增函数,且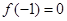 ,则不等式
,则不等式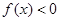 的解集为
的解集为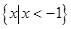 .
. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
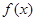 的定义域为
的定义域为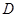 ,若存在闭区间
,若存在闭区间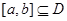 ,使得函数
,使得函数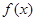 满足:①
满足:①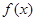 在
在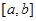 内是单调函数;②
内是单调函数;②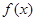 在
在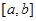 上的值域为
上的值域为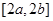 ,则称区间
,则称区间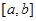 为
为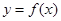 的“倍值区间”.下列函数中存在“倍值区间”的有
的“倍值区间”.下列函数中存在“倍值区间”的有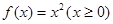 ; ②
; ②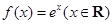 ;
;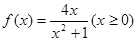 ; ④
; ④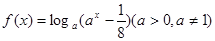
| A.①②③④ | B.①②④ | C.①③④ | D.①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com