
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(2)不妨设x1>x2,问题转化为$h'(x)=\frac{1}{x}-\frac{k}{x^2}=\frac{x-k}{x^2}≥0$,从而求出k的最小值,得到k的范围即可;
(3)求出函数h(x)的导数,通过讨论k的范围,求出函数的单调区间,得到函数的最小值,从而判断结论即可.
解答 解:(1)注意到函数f(x) 的定义域为$({0,+∞}),h(x)=lnx-\frac{{k({x-1})}}{x}({x>0})$,
当k=e 时,$h'(x)=\frac{1}{x}-\frac{e}{x^2}=\frac{x-e}{x^2}$,若0<x<e,则h'(x)<0;
若x>e,则h'(x)>0,所以h(x) 是(0,e)上的减函数,是(e,+∞)上的增函数,
故h(x)极小值=h(e)=2-e,故函数h(x)极小值为2-e,无极大值;…3分
(2)$\frac{f(x)}{x}=lnx$ 在[1,2]上是增函数,当k>0 时,$\frac{g(x)}{x}=\frac{{k({x-1})}}{x}=k({1-\frac{1}{x}})$ 在[1,2]上是增函数,
不妨设x1>x2,则$\frac{{f({x_1})}}{x_1}-\frac{{f({x_2})}}{x_2}>\frac{{g({x_1})}}{x_1}-\frac{{g({x_2})}}{x_2}$,$\frac{{f({x_1})}}{x_1}-\frac{{g({x_1})}}{x_1}>\frac{{f({x_2})}}{x_2}-\frac{{g({x_2})}}{x_2}$ …5分
设$h(x)=\frac{f(x)}{x}-\frac{g(x)}{x}=lnx-\frac{{k({x-1})}}{x}({1≤x≤2})$ 在[1,2]上是增函数
转化为$h'(x)=\frac{1}{x}-\frac{k}{x^2}=\frac{x-k}{x^2}≥0$,
在[1,2]上恒成立,k≤(x)min=1,故实数k 的取值范围为(0,1]…8分
(3)$h'(x)=\frac{1}{x}-\frac{k}{x^2}=\frac{x-k}{x^2}$,当k≤0 时,h'(x)>0 对x>0 恒成立,
所以h(x) 是(0,+∞) 上的增函数,h(x) 是[1,e]上的增函数,
h(x)min=h(1)=0,不合题意,…9分
当k>0 时,若0<x<k,h'(x)<0;若x>k,h'(x)>0;
所以h(x) 是(0,k) 上的减函数,是(k,+∞) 上的增函数,…10分
(ⅰ)当k≥e 时,h(x) 是[1,e]上的减函数,$h{(x)_{min}}=h(e)=1-\frac{k(e-1)}{e}$,
令$1-\frac{k(e-1)}{e}=\frac{1}{2}$,解得$k=\frac{e}{{2({e-1})}}$,不满足k≥e,舍去. …11分
(ⅱ)当1<k<e,h(x) 是(1,k) 上的减函数,是(k,e) 上的增函数,
h(x)min=h(k)=lnk-k+1 …12分
令$μ(x)=lnx-x+1({x>0}),μ'(x)=\frac{1}{x}-1=\frac{1-x}{x}$,当0<x<1 时,μ'(x)>0;
当x>1 时,μ'(x)<0.所以μ(x) 是(0,1)上的增函数,是(1,+∞) 上的减函数,
故μ(x)≤μ(1)=0 当且仅当x=1 时等号成立,h(x)min=h(k)=lnk-k+1≤0,
故最小值不是$\frac{1}{2}$,不合题意.…14分
(ⅲ)当0<k≤1 时,h(x) 是[1,e]上的增函数,h(x)min=h(1)=0,不合题意,…15分
综上,不存在实数k,使得函数h(x)=f(x)-g(x) 在[1,e]上的最小值为$\frac{1}{2}$ …16分.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,考查学生的分析问题的能力和计算能力,是一道综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 若p∨q为真命题,则p∧q为真命题. | |
| B. | “x=5”是“x2-4x-5=0”的必要不充分条件. | |
| C. | 命题“?x∈R,x2+x-1<0”的否定为:“?x∈R,x2+x-1≥0”. | |
| D. | 命题“已知A,B为一个三角形两内角,若A=B,则sinA=sinB”的否命题为真命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}+\frac{y^2}{3}=1$ | B. | $\frac{x^2}{6}+\frac{y^2}{3}=1$ | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ac>bc,则a>b | B. | 若a<b,则ac2<bc2 | ||
| C. | 若$\frac{1}{a}$<$\frac{1}{b}$<0,则a>b | D. | 若a>b,c>d,则a-c>b-d |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
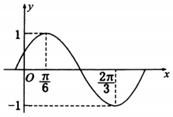 函数f(x)=Asin(ωx+φ)(A>0,ω,0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω,0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com