
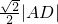 ,且△ABC的面积为20,求直线BC的方程.
,且△ABC的面积为20,求直线BC的方程.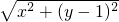 =|y+1|,
=|y+1|, x2,∴y′=
x2,∴y′= x,
x,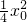 ),由导数的几何意义 得直线l的斜率为kBC=
),由导数的几何意义 得直线l的斜率为kBC=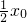 ,
,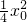 ),设C(x1,
),设C(x1,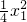 ),B(x2,
),B(x2, ).
).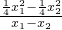 =
= =
= x0,∴x1+x2=2x0.
x0,∴x1+x2=2x0.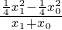 =
= ,kAB=
,kAB=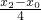 ,
, +
+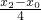 =
=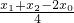 =0,∴kAB=-kBC.
=0,∴kAB=-kBC.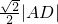 ,可知∠BAD=45°,
,可知∠BAD=45°,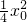 =-(x+x0),与x2=-4y联立方程组,
=-(x+x0),与x2=-4y联立方程组,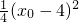 ),∴|AB|=
),∴|AB|= |x0-4-(-x0)|=2
|x0-4-(-x0)|=2 |x0-2|
|x0-2| |x0+2|.
|x0+2|. ×
× |x0+2|×2
|x0+2|×2 |x0-2|=20.
|x0-2|=20. ),KBC=
),KBC= ,直线BC的方程为6x-4y+7=0;
,直线BC的方程为6x-4y+7=0;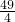 ),KBC=-
),KBC=- ,直线BC的方程为6x+4y-7=0;
,直线BC的方程为6x+4y-7=0; x2,设D(x0,
x2,设D(x0,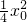 ),由导数的几何意义,得直线l的斜率,又A(-x0,
),由导数的几何意义,得直线l的斜率,又A(-x0,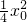 ),设C(x1,
),设C(x1,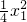 ),B(x2,
),B(x2, ).利用斜率公式得到x1+x2=2x0.从而有kAB=-kBC,即可证得∠BAD=∠CAD.
).利用斜率公式得到x1+x2=2x0.从而有kAB=-kBC,即可证得∠BAD=∠CAD.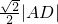 ,可知∠BAD=45°,将直线AB的方程与x2=-4y联立方程组,解得B点的坐标,求出|AB|,|AC|,最后根据△ABC的面积列出方程,解得x0=±3,从而得出直线BC的方程.
,可知∠BAD=45°,将直线AB的方程与x2=-4y联立方程组,解得B点的坐标,求出|AB|,|AC|,最后根据△ABC的面积列出方程,解得x0=±3,从而得出直线BC的方程.

科目:高中数学 来源: 题型:
| A、有最大值为π | B、有最小值为π | C、有最大值为4π | D、有最小值为4π |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com