
分析 由题意,方程可化为7x2-(13+m)x-(m+2)=0;令f(x)=7x2-(13+m)x-(m+2),从而可得$\left\{\begin{array}{l}{f(0)=-(m+2)>0}\\{f(1)=7-(13+m)-(m+2)<0}\\{f(2)=28-2(13+m)-(m+2)>0}\end{array}\right.$;从而解得.
解答 解:∵${2}^{7{x}^{2}-13x-m}$=($\frac{1}{2}$)-mx-2,
∴${2}^{7{x}^{2}-13x-m}$=2mx+2,
∴7x2-13x-m=mx+2;
即7x2-(13+m)x-(m+2)=0;
令f(x)=7x2-(13+m)x-(m+2),
又∵7x2-(13+m)x-(m+2)=0的一个根在区间(0,1)内,另一个根在区间(1,2)内,
∴$\left\{\begin{array}{l}{f(0)=-(m+2)>0}\\{f(1)=7-(13+m)-(m+2)<0}\\{f(2)=28-2(13+m)-(m+2)>0}\end{array}\right.$;
∴-4<m<-2;
故答案为:(-4,-2).
点评 本题考查了方程的化简与方程的根与函数的零点的关系应用,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{\sqrt{2}x′=\sqrt{5}x}\\{y′=\sqrt{2}y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\sqrt{2}x′=x}\\{\sqrt{5}y′=\sqrt{2}y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{\sqrt{5}x′=\sqrt{2}x}\\{\sqrt{2}y′=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5x′=2x}\\{\sqrt{2}y′=y}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 下表是随机抽取的某市五个地段五种不同户型新电梯房面积x(单位:十平方米)和相应的房价y(单位:万元)统计表:
下表是随机抽取的某市五个地段五种不同户型新电梯房面积x(单位:十平方米)和相应的房价y(单位:万元)统计表:| x | 7 | 9 | 10 | 11 | 13 |
| y | 40 | 75 | 70 | 90 | 105 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
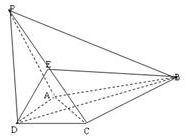 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 25 | ||
| 学习积极性一般 | 25 | ||
| 合计 | 24 | 26 | 50 |
| P(K2≥K0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b都能被5整除 | B. | a,b有1个不能被5整除 | ||
| C. | a不能被5整除 | D. | a,b都不能被5整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 670 | B. | 671 | C. | 1341 | D. | 1342 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com