
 的图象与
的图象与 的图象关于y轴对称.
的图象关于y轴对称. (a∈R),试讨论函数g(x)的单调性.
(a∈R),试讨论函数g(x)的单调性. 的图象关于y轴对称的图象对应的解析式,进而可得m的值;
的图象关于y轴对称的图象对应的解析式,进而可得m的值;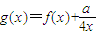 的解析式,求出其导函数,分类讨论可得函数的单调性.
的解析式,求出其导函数,分类讨论可得函数的单调性.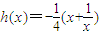 的图象关于y轴对称的图象对应的解析式为:
的图象关于y轴对称的图象对应的解析式为: =
=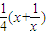
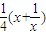
 =
=
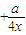 =
=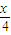 +
+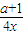
 -
-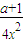 =
=
 )∪(
)∪(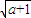 ,+∞)时,g′(x)>0;
,+∞)时,g′(x)>0;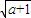 ,
,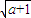 )时,g′(x)<0;
)时,g′(x)<0;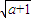 )和(
)和(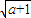 ,+∞)上为增函数;
,+∞)上为增函数; ,
,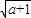 )上为减函数;
)上为减函数;

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源:2011-2012学年福建省泉州市高三(下)第二次质量检测数学试卷(文科)(解析版) 题型:解答题
 的图象与x轴相切于点S(s,0).
的图象与x轴相切于点S(s,0). .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省东莞市高三模拟(一)文科数学试卷(解析版) 题型:填空题
在同一平面直角坐标系中,已知函数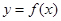 的图象与
的图象与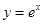 的图象关于直线
的图象关于直线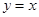 对称,则函数
对称,则函数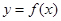 对应的曲线在点(
对应的曲线在点(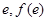 )处的切线方程为
.
)处的切线方程为
.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高三第四次模拟考试数学试题 题型:填空题
在同一平面直角坐标系中,已知函数 的图象与
的图象与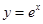 的图象关于直线
的图象关于直线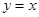 对称,则函数
对称,则函数 对应的曲线在点(
对应的曲线在点( )处的切线方程为
.
)处的切线方程为
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com