
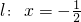 相切,并且经过点
相切,并且经过点 ,
,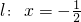 相切,并且经过点
相切,并且经过点 ,
, 的距离等于θ到定直线
的距离等于θ到定直线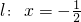 的距离,都等于圆的半径…(2分)
的距离,都等于圆的半径…(2分) =
= ,解得p=1
,解得p=1 .…(9分)
.…(9分)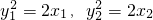 ,可得y1y2=
,可得y1y2=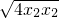 =2
=2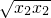 =4.…(10分)
=4.…(10分)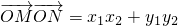 =4-4=0,
=4-4=0, 夹角为90°,即OM⊥ON.…(12分)
夹角为90°,即OM⊥ON.…(12分) =0,所以
=0,所以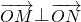 ,使结论得证.
,使结论得证.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
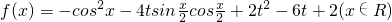
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 10 | 25 | 35 | 30 | x |
| 分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 15 | 30 | 25 | y | 5 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
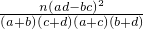 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 评价等级(分) | 0-1.0 | 1.1-2.0 | 2.1-3.0 | 3.1-4.0 | 4.1-5.0 |
| 女(人数) | 2 | 7 | 9 | 20 | 12 |
| 男(人数) | 3 | 9 | 18 | 12 | 8 |
| 喜欢该商品 | 不喜欢该商品 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
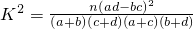 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com