
在△ABC中,若sin2A+sin2B<sin2C,则△ABC的形状是( )
(A)钝角三角形 (B)直角三角形
(C)锐角三角形 (D)不能确定
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十八第四章第四节练习卷(解析版) 题型:填空题
如图,已知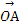 =a,
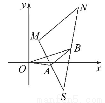
=a,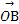 =b,任意点M关于点A的对称点为S,点S关于点B的对称点为N.设|a|=1,|b|=2,a与b的夹角为30°,若
=b,任意点M关于点A的对称点为S,点S关于点B的对称点为N.设|a|=1,|b|=2,a与b的夹角为30°,若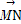 ⊥(λa+b),则实数λ= .
⊥(λa+b),则实数λ= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十二第三章第六节练习卷(解析版) 题型:选择题
函数y= sin2x+
sin2x+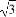 cos2x-
cos2x-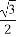 的最小正周期等于( )
的最小正周期等于( )
(A)π (B)2π (C) (D)
(D)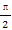
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十九第四章第五节练习卷(解析版) 题型:选择题
若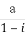 =1-bi,其中a,b都是实数,i是虚数单位,则|a+bi|=( )
=1-bi,其中a,b都是实数,i是虚数单位,则|a+bi|=( )
(A)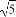 (B)
(B)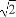 (C)
(C)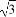 (D)1
(D)1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十七第四章第三节练习卷(解析版) 题型:填空题
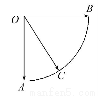
给定两个长度为1的平面向量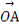 和
和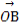 ,它们的夹角为90°.如图所示,点C在以O为圆心的圆弧
,它们的夹角为90°.如图所示,点C在以O为圆心的圆弧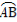 上运动,若
上运动,若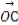 =x
=x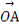 +y
+y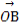 ,其中x,y∈R,则xy的范围是 .
,其中x,y∈R,则xy的范围是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十七第四章第三节练习卷(解析版) 题型:选择题
设a,b是不共线的两个向量,其夹角是θ,若函数f(x)=(xa+b)·(a-xb)(x∈R)在(0,+∞)上有最大值,则( )
(A)|a|<|b|,且θ是钝角
(B)|a|<|b|,且θ是锐角
(C)|a|>|b|,且θ是钝角
(D)|a|>|b|,且θ是锐角
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十一第三章第五节练习卷(解析版) 题型:选择题
已知向量a=(sin(α+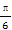 ),1),b=(4,4cosα-
),1),b=(4,4cosα-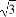 ),若a⊥b,则sin(α+
),若a⊥b,则sin(α+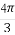 )=( )
)=( )
(A)-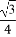 (B)-
(B)- (C)
(C)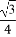 (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十六第六章第二节练习卷(解析版) 题型:填空题
已知集合A={x∈R||x+2|<3},B={x∈R|(x-m)(x-2)<0},且A∩B=(-1,n),则m= ,n= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com