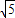【答案】
分析:将两圆的方程相减,得到一个二元一次方程,即为公共弦所在的直线方程,将圆C
2化为标准方程,找出圆心坐标和半径r,利用点到直线的距离公式求出圆心C
2到所求直线的距离d,利用垂径定理及勾股定理得到公共弦长为2
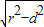
,求出即可.
解答:解:∵圆C
1的方程为x
2+y
2-2x+10y-24=0①,圆C
2的方程为x
2+y
2+2x+2y-8=0②,
∴①-②得:-4x+8y-16=0,即公共弦所在直线的方程x-2y+4=0,
又将圆C
2化为标准方程得:(x+1)
2+(y+1)
2=10,
∴圆心C
2的坐标为(-1,-1),半径r=
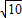
,
∴圆心C
2到此方程的距离d=
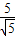
=
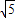
,
则公共弦的长为2
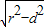
=2
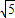
.
故答案为:2
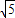 点评:
点评:此题考查了圆与圆位置关系的及其判定,涉及的知识有:圆的标准方程,点到直线的距离公式,垂径定理,以及勾股定理,解题的关键是将两圆方程相减求出公共弦所在直线的方程.

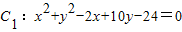 与
与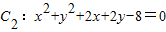 公共弦的长为 .
公共弦的长为 . 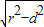 ,求出即可.
,求出即可.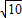 ,
,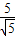 =
=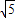 ,
,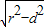 =2
=2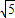 .
.