
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 是过点
是过点![]() ,倾斜角为
,倾斜角为![]() 的直线,以直角坐标系
的直线,以直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的一个参数方程;
的一个参数方程;
(Ⅱ)曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】网络直播是一种新兴的网络社交方式,网络直播平台也成为了一种崭新的社交媒体.很多人选择在快手、抖音等网络直播平台上分享自己的生活点滴.2020年的寒假,注定不凡.因为新冠病毒疫情的影响,开学延迟了,老师们停课不停教,在网络上直播授课;同学们停课不停学,在家上网课.某网络社交平台为了了解网络直播在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你直播过吗?”其中,回答“直播过”的共有![]() 个人.把这
个人.把这![]() 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.

(1)求![]() 和
和![]() 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交警随机抽取了途径某服务站的40辆小型轿车在经过某区间路段的车速(单位: ![]() ),现将其分成六组为
),现将其分成六组为![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.
(1)某小型轿车途经该路段,其速度在![]() 以上的概率是多少?
以上的概率是多少?
(2)若对车速在![]() 两组内进一步抽测两辆小型轿车,求至少有一辆小型轿车速度在
两组内进一步抽测两辆小型轿车,求至少有一辆小型轿车速度在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是一个非空集合,
是一个非空集合, ![]() 是定义在
是定义在![]() 上的一个运算.如果同时满足下述四个条件:
上的一个运算.如果同时满足下述四个条件:
(1)对于![]() ,都有
,都有![]() ;
;
(2)对于![]() ,都有
,都有![]() ;
;
(3)对于![]() ,使得
,使得![]() ;
;
(4)对于![]() ,使得
,使得![]() (注:“
(注:“![]() ”同(iii)中的“
”同(iii)中的“![]() ”).
”).
则称![]() 关于运算
关于运算![]() 构成一个群.现给出下列集合和运算:
构成一个群.现给出下列集合和运算:
①![]() 是整数集合,
是整数集合, ![]() 为加法;②
为加法;②![]() 是奇数集合,
是奇数集合, ![]() 为乘法;③
为乘法;③![]() 是平面向量集合,
是平面向量集合, ![]() 为数量积运算;④
为数量积运算;④![]() 是非零复数集合,
是非零复数集合, ![]() 为乘法. 其中
为乘法. 其中![]() 关于运算
关于运算![]() 构成群的序号是___________(将你认为正确的序号都写上).
构成群的序号是___________(将你认为正确的序号都写上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱AB与底面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂直,路灯C采用锥形灯罩,射出的管线与平面ABC部分截面如图中阴影所示,![]() 路宽AD=24米,设
路宽AD=24米,设![]()

(1)求灯柱AB的高h(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学参加社会实践活动,随机调查了某小区5个家庭的年可支配收入x(单位:万元)与年家庭消费y(单位:万元)的数据,制作了对照表:
x/万元 | 2.7 | 2.8 | 3.1 | 3.5 | 3.9 |
y/万元 | 1.4 | 1.5 | 1.6 | 1.8 | 2.2 |
由表中数据得回归直线方程为![]() ,得到下列结论,其中正确的是( )
,得到下列结论,其中正确的是( )
A.若某户年可支配收入为4万元时,则年家庭消费约为2.3万元
B.若某户年可支配收入为4万元时,则年家庭消费约为2.1万元
C.若年可支配收入每增加1万元,则年家庭消费相应平均增加0.5万元
D.若年可支配收入每增加1万元,则年家庭消费相应平均增加0.1万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世界卫生组织设定的最宽限值,即
标准采用世界卫生组织设定的最宽限值,即![]() 日均值在
日均值在![]() 以下空气质量为优;在
以下空气质量为优;在![]() 之间空气质量为良;在
之间空气质量为良;在![]() 之间空气质量为轻度污染.某市环保局从该市2018年上半年每天的
之间空气质量为轻度污染.某市环保局从该市2018年上半年每天的![]() 日均值数据中随机抽取20天的数据作为样本,将
日均值数据中随机抽取20天的数据作为样本,将![]() 日均值统计如下:
日均值统计如下:
日均值( |
|
|
|
|
|
天数 | 4 | 6 | 5 | 3 | 2 |
(1)在空气质量为轻度污染的数据中,随机抽取两天![]() 日均值数据,求其中恰有一天
日均值数据,求其中恰有一天![]() 日均值数据在
日均值数据在![]() 之间的概率;
之间的概率;
(2)将以上样本数据绘制成频率分布直方图(直接作图):
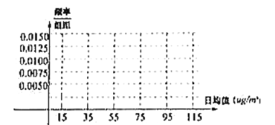
(3)该市规定:全年![]() 日均值的平均数不高于
日均值的平均数不高于![]() ,则认定该市当年的空气质量达标.现以这20天的
,则认定该市当年的空气质量达标.现以这20天的![]() 日均值的平均数来估计2018年的空气质量情况,试预测该市2018年的空气质量是否达标.
日均值的平均数来估计2018年的空气质量情况,试预测该市2018年的空气质量是否达标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com