
【题目】若数列![]() 满足n≥2时,
满足n≥2时,![]() ,则称数列
,则称数列![]() (n
(n![]() )为
)为![]() 的“L数列”.
的“L数列”.
(1)若![]() ,且
,且![]() 的“L数列”为
的“L数列”为![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 的“L数列”为递增数列,求k的取值范围;
的“L数列”为递增数列,求k的取值范围;
(3)若![]() ,其中p>1,记
,其中p>1,记![]() 的“L数列”的前n项和为
的“L数列”的前n项和为![]() ,试判断是否存在等差数列
,试判断是否存在等差数列![]() ,对任意n
,对任意n![]() ,都有
,都有![]() 成立,并证明你的结论.
成立,并证明你的结论.
【答案】(1)![]() ;(2)(1,+∞);(3)存在满足条件的等差数列
;(2)(1,+∞);(3)存在满足条件的等差数列![]() ,见解析
,见解析
【解析】
(1)由题意知![]() 即
即![]() ,利用累乘法即可求得通项公式;(2)由
,利用累乘法即可求得通项公式;(2)由![]() 可得
可得![]() ,设
,设![]() ,根据题意{bn}为递增数列,只需
,根据题意{bn}为递增数列,只需![]() -
-![]() >0恒成立即可求得满足题意的k值;(3)根据
>0恒成立即可求得满足题意的k值;(3)根据![]() 的通项公式求出
的通项公式求出![]() ,利用放缩法及等比数列的前n项和公式可得
,利用放缩法及等比数列的前n项和公式可得![]() ,再次利用
,再次利用![]() 放缩可得
放缩可得![]() ,设
,设![]() ,易证其为等差数列,结论成立.
,易证其为等差数列,结论成立.
(1)由题意知,![]() 即
即![]() ,
,
所以![]() ,
,
即数列![]() 的通项公式为
的通项公式为![]() .
.
(2)因为![]() ,且n≥2,n∈N*时,
,且n≥2,n∈N*时,![]() ,所以
,所以![]() ,
,
设![]() ,n∈N*,所以
,n∈N*,所以![]() 1-
1-![]() .
.
因为{bn}为递增数列,所以![]() 对n∈N*恒成立,
对n∈N*恒成立,
即![]() -
-![]() >0对
>0对![]() 恒成立.
恒成立.
因为![]() -
-![]() =
=![]() ,
,
所以![]() -
-![]() >0等价于
>0等价于![]() .
.
当0<k≤1时,因为n=1时,![]() ,不符合题意.
,不符合题意.
当k>1时,![]() ,所以
,所以![]() ,
,
综上,k的取值范围是![]() .
.
(3)存在满足条件的等差数列![]() ,证明如下:
,证明如下:
因为 ,k
,k![]() ,
,
所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
即![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
设![]() ,则
,则![]() ,且
,且![]() ,
,
所以存在等差数列![]() 满足题意.
满足题意.


科目:高中数学 来源: 题型:
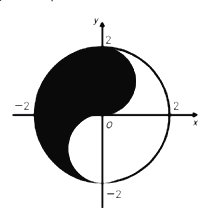
【题目】众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”.整个图形是一个圆形.其中黑色阴影区域在y轴右侧部分的边界为一个半圆,给出以下命题:
①在太极图中随机取一点,此点取自黑色阴影部分的概率是![]()
②当![]() 时,直线y=ax+2a与白色部分有公共点;
时,直线y=ax+2a与白色部分有公共点;
③黑色阴影部分(包括黑白交界处)中一点(x,y),则x+y的最大值为2;
④设点P(﹣2,b),点Q在此太极图上,使得∠OPQ=45°,b的范围是[﹣2,2].
其中所有正确结论的序号是( )
A.①④B.①③C.②④D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受突如其来的新冠疫情的影响,全国各地学校都推迟2020年的春季开学.某学校“停课不停学”,利用云课平台提供免费线上课程.该学校为了解学生对线上课程的满意程度,随机抽取了500名学生对该线上课程评分.其频率分布直方图如下:若根据频率分布直方图得到的评分低于80分的概率估计值为0.45.
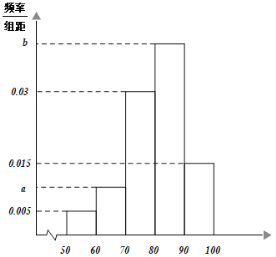
(1)(i)求直方图中的a,b值;
(ii)若评分的平均值和众数均不低于80分视为满意,判断该校学生对线上课程是否满意?并说明理由(同一组中的数据用该组区间的中点值为代表);
(2)若采用分层抽样的方法,从样本评分在[60,70)和[90,100]内的学生中共抽取5人进行测试来检验他们的网课学习效果,再从中选取2人进行跟踪分析,求这2人中至少一人评分在[60,70)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过焦点且垂直于
.过焦点且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 相交所得的弦长为3,直线
相交所得的弦长为3,直线![]() 与椭圆
与椭圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,问直线
,问直线![]() 是否存在?若存在,求直线
是否存在?若存在,求直线![]() 的斜率
的斜率![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PAPD,E,F分别为AD,PB的中点.求证:
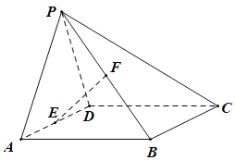
(1)EF//平面PCD;
(2)平面PAB平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,且
为平行四边形,且![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为60°,求平面
所成角为60°,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学计划用他姓名的首字母![]() ,身份证的后4位数字(4位数字都不同)以及3个符号
,身份证的后4位数字(4位数字都不同)以及3个符号![]() 设置一个六位的密码.若
设置一个六位的密码.若![]() 必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
A.864B.1009C.1225D.1441
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程:
的参数方程: (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)过曲线![]() 上一点
上一点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,中点为
两点,中点为![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国新型冠状病毒肺炎疫情期间,以网络购物和网上服务所代表的新兴消费展现出了强大的生命力,新兴消费将成为我国消费增长的新动能.某市为了了解本地居民在2020年2月至3月两个月网络购物消费情况,在网上随机对1000人做了问卷调查,得如下频数分布表:
网购消费情况(元) |
|
|
|
|
|
频数 | 300 | 400 | 180 | 60 | 60 |
(1)作出这些数据的频率分布直方图,并估计本市居民此期间网络购物的消费平均值;
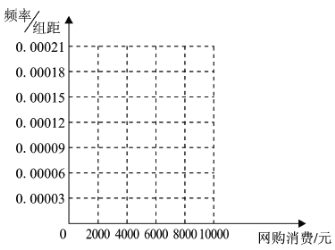
(2)在调查问卷中有一项是填写本人年龄,为研究网购金额和网购人年龄的关系,以网购金额是否超过4000元为标准进行分层抽样,从上述1000人中抽取200人,得到如下列联表,请将表补充完整并根据列联表判断,在此期间是否有95%的把握认为网购金额与网购人年龄有关.
网购不超过4000元 | 网购超过4000元 | 总计 | |
40岁以上 | 75 | 100 | |
40岁以下(含40岁) | |||
总计 | 200 |
参考公式和数据:![]() .(其中
.(其中![]() 为样本容量)
为样本容量)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com