
【题目】如图,在四棱锥P—ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PAPD,E,F分别为AD,PB的中点.求证:
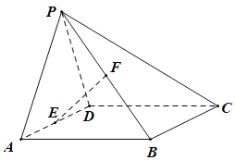
(1)EF//平面PCD;
(2)平面PAB平面PCD.
科目:高中数学 来源: 题型:
【题目】平面凸六边形![]() 的边长相等,其中
的边长相等,其中![]() 为矩形,
为矩形,![]() .将
.将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折至
折至![]() ,
,![]() ,且均在同侧与平面
,且均在同侧与平面![]() 垂直,连接
垂直,连接![]() ,如图所示,E,G分别是
,如图所示,E,G分别是![]() ,
,![]() 的中点.
的中点.
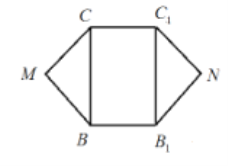
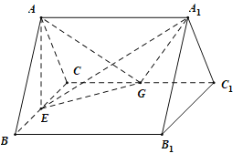
(1)求证:多面体![]() 为直三棱柱;
为直三棱柱;
(2)求二面角![]() 平面角的余弦值.
平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某地区小学的期末考试中抽取部分学生的数学成绩,由抽查结果得到如图的频率分布直方图,分数落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
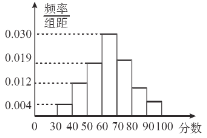
(1)求这些学生的分数落在区间![]() 内的频率;
内的频率;
(2)若将频率视为概率,从该地区小学的这些学生中随机抽取3人,记这3人中成绩位于区间![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,A、B、C、D四地新增疑似病例数据信息如下:
A地:中位数为2,极差为5; B地:总体平均数为2,众数为2;
C地:总体平均数为1,总体方差大于0; D地:总体平均数为2,总体方差为3.
则以上四地中,一定符合没有发生大规模群体感染标志的是_______(填A、B、C、D)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足n≥2时,
满足n≥2时,![]() ,则称数列
,则称数列![]() (n
(n![]() )为
)为![]() 的“L数列”.
的“L数列”.
(1)若![]() ,且
,且![]() 的“L数列”为
的“L数列”为![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 的“L数列”为递增数列,求k的取值范围;
的“L数列”为递增数列,求k的取值范围;
(3)若![]() ,其中p>1,记
,其中p>1,记![]() 的“L数列”的前n项和为
的“L数列”的前n项和为![]() ,试判断是否存在等差数列
,试判断是否存在等差数列![]() ,对任意n
,对任意n![]() ,都有
,都有![]() 成立,并证明你的结论.
成立,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,其焦点到准线的距离为2.直线
,其焦点到准线的距离为2.直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 与
与![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六,八是中国人的吉利数字,所以好多器都做成六棱形和八棱形,数学李老师有一个正六棱柱形状的笔筒,底面边长为6cm,高为18cm(底部及筒壁厚度忽略不计),一长度为![]() cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有教师400人,其中高中教师240人.为了了解该校教师每天课外锻炼时间,现利用分层抽样的方法从该校教师中随机抽取了100名教师进行调查,统计其每天课外锻炼时间(所有教师每天课外锻炼时间均在![]() 分钟内),将统计数据按
分钟内),将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分成6组,制成频率分布直方图如下:
分成6组,制成频率分布直方图如下:
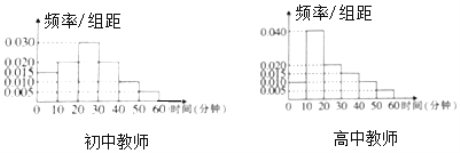
假设每位教师每天课外锻炼时间相互独立,并称每天锻炼时间小于20分钟为缺乏锻炼.
(1)试估计本校教师中缺乏锻炼的人数;
(2)若从参与调查,且每天课外锻炼时间在![]() 内的该校教师中任取2人,求至少有1名初中教师被选中的概率.
内的该校教师中任取2人,求至少有1名初中教师被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com