
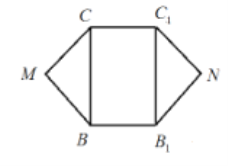
【题目】平面凸六边形![]() 的边长相等,其中
的边长相等,其中![]() 为矩形,
为矩形,![]() .将
.将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折至
折至![]() ,
,![]() ,且均在同侧与平面
,且均在同侧与平面![]() 垂直,连接
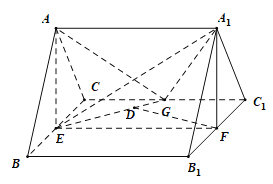
垂直,连接![]() ,如图所示,E,G分别是
,如图所示,E,G分别是![]() ,
,![]() 的中点.
的中点.
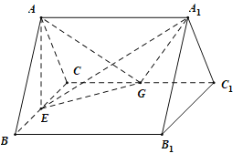
(1)求证:多面体![]() 为直三棱柱;
为直三棱柱;
(2)求二面角![]() 平面角的余弦值.
平面角的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1) 取![]() 中点F,连接
中点F,连接![]() ,
,![]() ,再证明四边形
,再证明四边形![]() 为平行四边形,进而根据平行四边形的性质证得平面
为平行四边形,进而根据平行四边形的性质证得平面![]() 平面
平面![]() ,同时证得侧棱
,同时证得侧棱![]() 且互相相等,再证明
且互相相等,再证明![]() 平面
平面![]() 即可.
即可.
(2) 过F作![]() 交
交![]() 于点D,连接
于点D,连接![]() ,根据线面垂直的性质可得
,根据线面垂直的性质可得![]() 为二面角
为二面角![]() 的平面角以及二面角
的平面角以及二面角![]() 的平面角为
的平面角为![]() ,进而根据三角形中的边长关系结合勾股定理求解即可.
,进而根据三角形中的边长关系结合勾股定理求解即可.
(1)证明:取![]() 中点F,连接
中点F,连接![]() ,
,![]() .
.
∵F为![]() 中点,
中点,![]() ,又面
,又面![]() 平面
平面![]() ,
,
且面![]() 平面
平面![]() ,
,![]()
∴![]() 平面
平面![]() .
.

同理可证![]() 平面
平面![]() ,
,![]() ,而
,而![]() ,故四边形
,故四边形![]() 为平行四边形,从而
为平行四边形,从而![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,故
,故![]() 且
且![]() ,因此四边形
,因此四边形![]() 为平面四边形,则
为平面四边形,则![]() ,
,
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ;
;
由题设显然有![]() 平面
平面![]() ,而
,而![]() ,故平面
,故平面![]() 平面
平面![]() ,
,
又四边形![]() ,
,![]() 为平行四边形,则
为平行四边形,则![]() ,从而四边形
,从而四边形![]() 为平行四边形,而
为平行四边形,而![]() 平面
平面![]() ,因此多面体
,因此多面体![]() 为直三棱柱;
为直三棱柱;
(2)过F作![]() 交
交![]() 于点D,连接
于点D,连接![]() .
.
由(1)![]() 平面
平面![]() 知
知![]() ,而
,而![]() ,
,![]() ,因此
,因此![]() 平面
平面![]() ,则
,则![]() ,
,
故![]() 为二面角
为二面角![]() 的平面角,
的平面角,
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() ,
,
因此二面角![]() 的平面角为
的平面角为![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
从而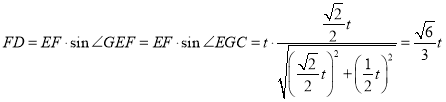 ,
,
故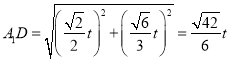 ,
,
则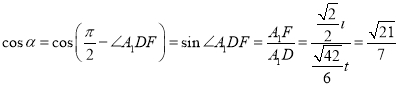


科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,![]() ,将
,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,
,![]() 为
为![]() 的中点.
的中点.
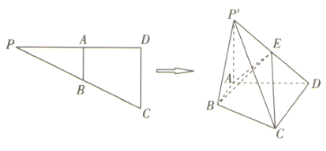
(1)证明:![]() 平面
平面![]() ;
;
(2)当正视图方向与向量![]() 的方向相同时,
的方向相同时,![]() 的正视图为直角三角形,求此时二面角
的正视图为直角三角形,求此时二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六,八是中国人的吉利数字,所以好多器都做成六棱形和八棱形,数学李老师有一个正六棱柱形状的笔筒,底面边长为6cm,高为18cm(底部及筒壁厚度忽略不计),一长度为![]() cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知点
中,已知点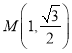 ,
,![]() 的参数方程为
的参数方程为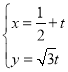 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月25日.阿里巴巴在杭州云栖大会上正式对外发布了含光800AI芯片,在业界标准的ResNet -50测试中,含光800推理性能达到78563lPS,比目前业界最好的AI芯片性能高4倍;能效比500 IPS/W,是第二名的3.3倍.在国内集成电路产业发展中,集成电路设计产业始终是国内集成电路产业中最具发展活力的领域,增长也最为迅速.如图是2014-2018年中国集成电路设计产业的销售额(亿元)及其增速(%)的统计图,则下面结论中正确的是( )
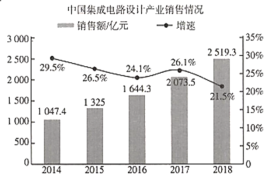
A.2014-2018年,中国集成电路设计产业的销售额逐年增加
B.2014-2017年,中国集成电路设计产业的销售额增速逐年下降
C.2018年中国集成电路设计产业的销售额的增长率比2015年的高
D.2018年与2014年相比,中国集成电路设计产业销售额的增长率约为110%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”.整个图形是一个圆形.其中黑色阴影区域在y轴右侧部分的边界为一个半圆,给出以下命题:
①在太极图中随机取一点,此点取自黑色阴影部分的概率是![]()
②当![]() 时,直线y=ax+2a与白色部分有公共点;
时,直线y=ax+2a与白色部分有公共点;
③黑色阴影部分(包括黑白交界处)中一点(x,y),则x+y的最大值为2;
④设点P(﹣2,b),点Q在此太极图上,使得∠OPQ=45°,b的范围是[﹣2,2].
其中所有正确结论的序号是( )
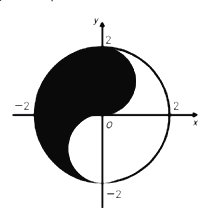
A.①④B.①③C.②④D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=1,∠ABD=60°,现将长方形ABCD沿着对角线BD折起,使平面ABD⊥平面BCD,则折后几何图形的外接球表面积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行的“新冠肺炎”防控知识闭卷考试比赛,总分获得一等奖、二等奖、三等奖的代表队人数情况如下表,该校政教处为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中一等奖代表队有6人.
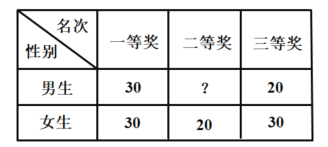
(1)求二等奖代表队的男生人数;
(2)从前排就坐的三等奖代表队员5人(2男3女)中随机抽取3人上台领奖,请求出只有一个男生上台领奖的概率;
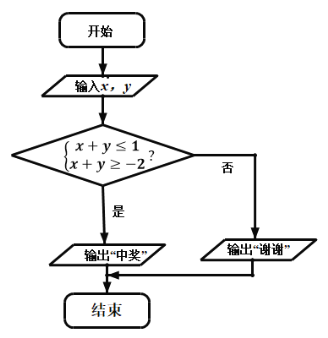
(3)抽奖活动中,代表队员通过操作按键,使电脑自动产生[![]() 2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PAPD,E,F分别为AD,PB的中点.求证:
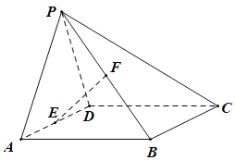
(1)EF//平面PCD;
(2)平面PAB平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com