
【题目】在直角坐标系![]() 中,已知点
中,已知点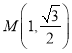 ,
,![]() 的参数方程为
的参数方程为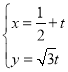 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】2019冠状病毒病(CoronaVirus Disease2019(COVID-19))是由新型冠状病毒(2019-nCoV)引发的疾病,目前全球感染者以百万计,我国在党中央、国务院、中央军委的坚强领导下,已经率先控制住疫情,但目前疫情防控形势依然严峻,湖北省中小学依然延期开学,所有学生按照停课不停学的要求,居家学习.小李同学在居家学习期间,从网上购买了一套高考数学冲刺模拟试卷,快递员计划在下午4:00~5:00之间送货到小区门口的快递柜中,小李同学父亲参加防疫志愿服务,按规定,他换班回家的时间在下午4:30~5:00,则小李父亲收到试卷无需等待的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某大型厂区有三个值班室![]() ,值班室
,值班室![]() 在值班室
在值班室![]() 的正北方向
的正北方向![]() 千米处,值班室
千米处,值班室![]() 在值班室
在值班室![]() 的正东方向
的正东方向![]() 千米处.
千米处.
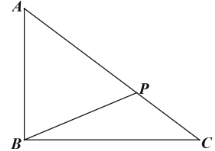
(1)保安甲沿![]() 从值班室
从值班室![]() 出发行至点
出发行至点![]() 处,此时
处,此时![]() ,求
,求![]() 的距离;
的距离;
(2)保安甲沿![]() 从值班室
从值班室![]() 出发前往值班室
出发前往值班室![]() ,保安乙沿
,保安乙沿![]() 从值班室
从值班室![]() 出发前往值班室
出发前往值班室![]() ,甲乙同时出发,甲的速度为
,甲乙同时出发,甲的速度为![]() 千米/小时,乙的速度为
千米/小时,乙的速度为![]() 千米/小时,若甲乙两人通过对讲机联系,对讲机在厂区内的最大通话距离为
千米/小时,若甲乙两人通过对讲机联系,对讲机在厂区内的最大通话距离为![]() 千米(含
千米(含![]() 千米),试问有多长时间两人不能通话?
千米),试问有多长时间两人不能通话?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为2的等边![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,将AED沿
的中点,将AED沿![]() 折起,使得
折起,使得![]() ,
, ![]() ,得到如图2的四棱锥A-BCDE,连结
,得到如图2的四棱锥A-BCDE,连结![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .
.
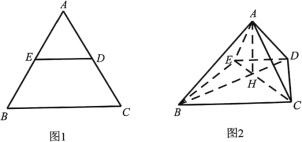
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代劳动人民在筑城、筑堤、挖沟、挖渠、建仓、建囤等工程中,积累了丰富的经验,总结出了一套有关体积、容积计算的方法,这些方法以实际问题的形式被收入我国古代数学名著《九章算术》中.《九章算术》将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,如图所示的阳马三视图,则它的体积为( )
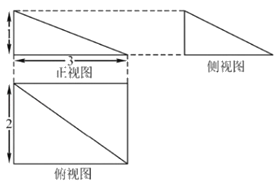
A.![]() B.1C.2D.3
B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com