分析:(Ⅰ)要证明BC⊥AB1,可证明AB1垂直于BC所在的平面BCD,已知CO垂直于侧面ABB1A1,所以CO垂直于AB1,只要在矩形ABB1A1内证明BD垂直于AB1即可,可利用角的关系加以证明;
(Ⅱ)求三棱锥B1-ABC的体积,可转化为求三棱锥C-ABB1 的体积,在Rt△ABD中,可求得BD的值和OA的值,从而三棱锥的体积可求.
解答: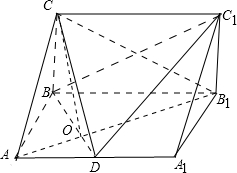
(Ⅰ)证明:如图,
因为ABB
1A
1是矩形,
D为AA
1中点,AB=1,
AA1=,AD=
,
所以在直角三角形ABB
1中,
tan∠AB1B==,
在直角三角形ABD中,
tan∠ABD==,
所以∠AB
1B=∠ABD,
又
∠BAB1+∠AB1B=90°,
∠BAB1+∠ABD=90°,
所以在直角三角形ABO中,故∠BOA=90°,
即BD⊥AB
1,
又因为CO⊥侧面ABB
1A
1,AB
1?侧面ABB
1A
1,
所以CO⊥AB
1所以,AB
1⊥面BCD,BC?面BCD,
故BC⊥AB
1.
(Ⅱ)解:在Rt△ABD中,可求得
BD=,
OC=OA===.
S△ABB1=AB•BB1=.
VB1-ABC=VC-ABB1=S△ABB1•OC=
••=
.
点评:本题考查了直线与平面垂直的性质,考查了利用等积法求棱锥的体积,考查空间想象能力、运算能力和推理论证能力,属于中档题.

 (2013•甘肃三模)在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=
(2013•甘肃三模)在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= (Ⅰ)证明:如图,
(Ⅰ)证明:如图,
