
已知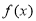 为定义在
为定义在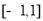 上的奇函数,当
上的奇函数,当 时,函数解析式为
时,函数解析式为 .
.
(Ⅰ)求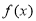 在
在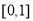 上的解析式;
上的解析式;
(Ⅱ)求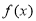 在
在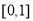 上的最值
上的最值
(Ⅰ)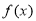
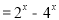
(Ⅱ)函数在[0,1]上的最大与最小值分别为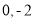 .
.
【解析】
试题分析:(Ⅰ)考查具有奇偶性的函数在某个区间上的解析式,求其在关于原点对称的区间上的解析式的问题,抓住关键点,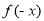 与
与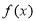 的关系即可;(Ⅱ)考查关于函数在某个区间上的最值问题的求解问题,注意式子的转化和整体思维的应用.
的关系即可;(Ⅱ)考查关于函数在某个区间上的最值问题的求解问题,注意式子的转化和整体思维的应用.
试题解析:(Ⅰ)设x∈ [0,1],则-x∈[-1,0].
∴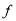 (-x)=
(-x)=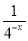 -
-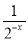 =4x-2x.
=4x-2x.
又∵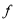 (-x)=-
(-x)=-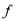 (x)
(x)
∴-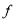 (x)=4x-2x.
(x)=4x-2x.
∴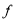 (x)
(x)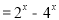
所以,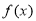 在
在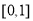 上的解析式为
上的解析式为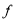 (x)
(x)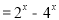 .
.
(Ⅱ)当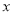 ∈[0,1],
∈[0,1],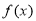 =2x-4x=2x-(2x)2,
=2x-4x=2x-(2x)2,
∴设t=2x(t>0),则f(t)=t-t2.
∵x∈[0,1],∴t∈[1,2].
当t=1时,取最大值,最大值为1-1=0.
当t=0时,取最小值为-2.
所以,函数在[0,1]上的最大与最小值分别为0,-2.
考点:1.具备奇偶性的函数的解析式的求解问题;2.有关指数函数和二次函数的复合函数在某个区间上的最值求解问题;3.整体思维的运用和换元的思想方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年吉林省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
关于 的不等式
的不等式 对
对 恒成立,则
恒成立,则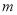 的取值范围( ).
的取值范围( ).
A.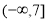 B.
B. C.
C. D.[-12,7]
D.[-12,7]
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省深圳市高一上学期期中考试数学试卷(解析版) 题型:解答题
设集合P= ,Q=
,Q=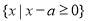
(1)若 ,求实数
,求实数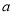 的取值范围;
的取值范围;
(2)若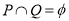 ;求实数
;求实数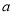 的取值范围;
的取值范围;
(3)若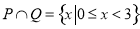 ,求实数
,求实数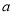 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版必修三 3.4互斥事件练习卷(解析版) 题型:?????
设事件A,B,已知P(A)= ,P(B)=
,P(B)= ,P(A∪B)=
,P(A∪B)=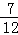 ,则A,B之间的关系一定为( )
,则A,B之间的关系一定为( )
A.互斥事件 B.两个任意事件 C.非互斥事件 D.对立事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com