
2cos2
| ||||
|
|
| tanA+tanB |
| 1-tanAtanB |
-
| ||
1+
|
| 3 |
| 5 |
| 3 |
| 5 |
2cos2
| ||||
|
| cosC+sinC |
| cosC-sinC |
| 1+tanC |
| 1-tanC |
1+
| ||
1-
|


科目:高中数学 来源: 题型:
| 1 |
| TD2 |
| 1 |
| TA2 |
| 1 |
| TB2 |
| 1 |
| TC2 |
| S | 2 △ABC |
| 1 |
| 3 |
| S | 2 △TAB |
| S | 2 △TAC |
| S | 2 △TBC |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三2月月考数学理卷 题型:填空题
已知在三棱锥T-ABC中,TA,TB,TC两两垂直,T在地面ABC上的投影为D,给出下列命题:
①TA⊥BC, TB⊥AC, TC⊥AB;
②△ABC是锐角三角形;
③ ;
;
④ (注:
(注: 表示△ABC的面积)
表示△ABC的面积)
其中正确的是_______(写出所有正确命题的编号)。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三2月月考数学理卷 题型:填空题
已知在三棱锥T-ABC中,TA,TB,TC两两垂直,T在地面ABC上的投影为D,给出下列命题:
①TA⊥BC, TB⊥AC, TC⊥AB;
②△ABC是锐角三角形;
③ ;
;
④ (注:
(注: 表示△ABC的面积)
表示△ABC的面积)
其中正确的是_______(写出所有正确命题的编号)。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省宜春市上高二中高三(下)第七次月考数学试卷(理科)(解析版) 题型:填空题
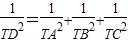 ;
; (注:S△ABC表示△ABC的面积)
(注:S△ABC表示△ABC的面积)查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都外国语学校高三(下)2月月考数学试卷(理科)(解析版) 题型:填空题
 ;
; (注:S△ABC表示△ABC的面积)
(注:S△ABC表示△ABC的面积)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com