练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (1＋2x)5的展开式中，x2的系数等于________．

     

    40

    【解析】(1＋2x)5的展开式的通项为

    Tr＋1＝C5r(2x)r＝2rC5r·xr，

    令r＝2，得22×C52＝4×10＝40.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届辽宁省大连市五校高二下学期期末考试文科数学试卷（解析版） 题型：选择题

    已知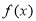是定义在R上的奇函数，当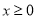时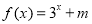（m为常数）,则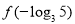的值为（ ）.

    A.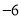 B.6 C.4 D.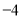

     

    查看答案和解析>>

    科目：高中数学 来源：2015届贵州省高二下学期期中文科数学试卷（解析版） 题型：填空题

    已知x与y之间的一组数据如下，则y与x的线性回归方程为y=bx+a，必过点 ．

    x

    1

    1

    2

    4

    y

    1

    4

    5

    6

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标模块练习卷（解析版） 题型：解答题

    为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：

    　　　　　性别

    是否需要志愿者 　　　　

    男

    女

    需要

    40

    30

    不需要

    160

    270

    (1)估计该地区老年人中，需要志愿者提供帮助的老年人的比例；

    (2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？

    (3)根据(2)的结论，能否提出更好的调查方法来估计该地区的老年人中，需要志愿者提供帮助的老年人的比例？说明理由．

    附：

    P(K2≥x0)

    0.050

    0.010

    0.001

    x0

    3.841

    6.635

    10.828

     

    χ2＝

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标模块练习卷（解析版） 题型：填空题

    随机抽取9个同学中，至少有2个同学在同一月出生的概率是________(默认每月天数相同，结果精确到0.001)．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标3章练习卷（解析版） 题型：解答题

    某企业有两个分厂生产某种零件，按规定内径尺寸(单位：mm)的值落在[29.94,30.06)的零件为优质品．从两个分厂生产的零件中各抽出了500件，量其内径尺寸，得结果如下表：

    甲厂：

    分组

    [29.86，29.90)

    [29.90，29.94)

    [29.94，29.98)

    [29.9830.02)，

    [30.02，30.06)

    [30.06，30.10)

    [30.10，30.14)

    频数

    12

    63

    86

    182

    92

    61

    4

    乙厂：

    分组

    [29.86，29.90)

    [29.90，29.94)

    [29.94，29.98)

    [29.9830.02)，

    [30.02，30.06)

    [30.06，30.10)

    [30.10，30.14)

    频数

    29

    71

    85

    159

    76

    62

    18

     

    (1)试分别估计两个分厂生产的零件的优质品率；

    (2)由以上统计数据填下面2×2列联表，并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”？

     

    甲厂

    乙厂

    合计

    优质品

     

     

     

    非优质品

     

     

     

    合　计

     

     

     

    附：

    P(χ2≥x0)

    0.05

    0.01

    x0

    3.841

    6.635

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标3章练习卷（解析版） 题型：填空题

    某单位为了解用电量y度与气温x℃之间的关系，随机统计了某4天的用电量与当天气温.

    气温(℃)

    14

    12

    8

    6

    用电量(度)

    22

    26

    34

    38

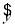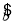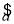    由表中数据得线性回归方程＝x＋中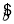＝－2，据此预测当气温为5 ℃时，用电量的度数约为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标3.2练习卷（解析版） 题型：填空题

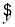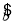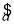    某小卖部为了了解冰糕销售量y(箱)与气温x(℃)之间的关系，随机统计了某4天卖出的冰糕的箱数与当天气温，并制作了对照表(如下表所示)，且由表中数据算得线性回归方程＝x＋中的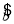＝2，则预测当气温为25 ℃时，冰糕销量为________箱.

    气温/℃

    18

    13

    10

    －1

    冰糕/箱

    64

    38

    34

    24

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.5练习卷（解析版） 题型：解答题

    A、B两个投资项目的利润率分别为随机变量X1和X2，根据市场分析，X1和X2的分布列分别为

    X1

    5%

    10%

    P

    0.8

    0.2

     

    X2

    2%

    8%

    12%

    P

    0.2

    0.5

    0.3

    (1)在A，B两个项目上各投资100万元，Y1和Y2分别表示投资项目A和B所获得的利润，求方差V(Y1)、V(Y2)；

    (2)将x(0≤x≤100)万元投资A项目，100－x万元投资B项目，f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和．求f(x)的最小值，并指出x为何值时，f(x)取到最小值．

     

    查看答案和解析>>

    同步练习册答案