
 为定义在
为定义在 上的奇函数,当
上的奇函数,当 时,
时, (
( 为常数),则
为常数),则 的值为( )
的值为( ) | A.-3 | B.-1 | C.1 | D.3 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
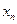 表示某鱼群在第
表示某鱼群在第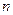 年初的总量,
年初的总量,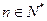 ,且
,且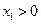 。不考虑其他因素,设在第
。不考虑其他因素,设在第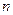 年内鱼群的繁殖量及被捕捞量都与
年内鱼群的繁殖量及被捕捞量都与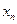 成正比,死亡量与
成正比,死亡量与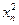 成正比,这些比例系数依次为正数
成正比,这些比例系数依次为正数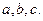 其中
其中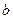 称为捕捞强度。
称为捕捞强度。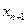 与
与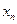 的关系式;
的关系式;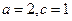 ,为了保证对任
,为了保证对任 意
意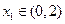 ,都有
,都有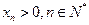 ,则捕捞强度
,则捕捞强度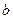 的最大允许值是多少?证明你的结论。
的最大允许值是多少?证明你的结论。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com