
| A. | $[-\frac{1}{2},\frac{1}{2}]$ | B. | $[-\sqrt{2},\sqrt{2}]$ | C. | $(-∞,-\sqrt{2})∪(\sqrt{2},+∞)$ | D. | [-1,1] |
分析 求出原函数的导函数,设出A,B的坐标,代入导函数,由函数在A,B处的导数等于0列式,换元后得到关于a的一元二次方程,结合线性规划知识求得a的取值范围.
解答 解:由f(x)=ax+sinx+cosx,得f′(x)=a+cosx-sinx,
设A(x1,y1),B(x2,y2),
则f′(x1)=a+cosx1-sinx1,f′(x2)=a+cosx2-sinx2.
由曲线y=f(x)在点A、B处的切线互相垂直,得
a2+[(cosx1-sinx1)+(cosx2-sinx2)]a+(cosx1-sinx1)(cosx2-sinx2)+1=0.
令m=cosx1-sinx1,n=cosx2-sinx2,
则m∈[-$\sqrt{2}$,$\sqrt{2}$],n∈[-$\sqrt{2}$,$\sqrt{2}$],
∴a2+(m+n)a+mn+1=0.
△=(m+n)2-4mn-4=(m-n)2-4,
∴0≤(m-n)2-4≤4.
当m-n=$±2\sqrt{2}$时,m+n=0,
又a=$\frac{-(m+n)±\sqrt{(m-n)^{2}-4}}{2}$.
∴-1≤a≤1.
∴函数f(x)的图象上存在不同的两点A,B,
使得曲线y=f(x)在点A,B处的切线互相垂直,则实数a的取值范围为[-1,1].
故选D.
点评 本题考查利用导数研究曲线上某点的切线方程,考查了数学转化思想方法,解答的关键在于由关于a的方程的根求解a的范围,是有一定难度题目.


科目:高中数学 来源: 题型:选择题
| A. | cosα | B. | sinα | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin($\frac{π}{3}$x+$\frac{π}{6}$) | B. | y=sin($\frac{π}{3}$x-$\frac{π}{6}$) | C. | y=cos($\frac{π}{3}$x+$\frac{π}{6}$) | D. | y=sin($\frac{π}{3}$x-$\frac{5π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$或$\frac{2}{3}$ | B. | $\frac{4}{3}$或$\frac{3}{4}$ | C. | $\frac{5}{3}或\frac{3}{5}$ | D. | $\frac{5}{4}或\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
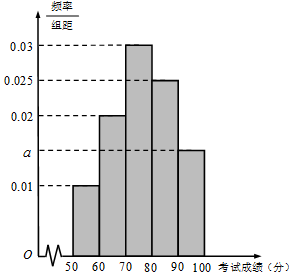 某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100],并绘制出频率分布直方图,如图所示.
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100],并绘制出频率分布直方图,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | -3 | C. | 3 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com