(Ⅰ)f(x)的定义域为(-∞,1)∪(1,+∞).对f(x)求导数得 f '(x)= e
-ax.
(ⅰ)当a=2时, f '(x)= e
-2x, f '(x)在(-∞,0), (0,1)和(1,+ ∞)均大于0,
所以f(x)在(-∞,1), (1,+∞).为增函数.
(ⅱ)当0<a<2时, f '(x)>0, f(x)在(-∞,1), (1,+∞)为增函数.
(ⅲ)当a>2时, 0<<1, 令f '(x)="0" ,解得x
1= - , x
2= .
当x变化时, f '(x)和f(x)的变化情况如下表:
x
| (-∞, -)
| (-,)
| (,1)
| (1,+∞)
|
f '(x)
| +
| -
| +
| +
|
f(x)
| ↗
| ↘
| ↗
| ↗
|
f(x)在(-∞, -), (,1), (1,+∞)为增函数,
f(x)在(-,)为减函数.
(Ⅱ)(ⅰ)当0<a≤2时, 由(Ⅰ)知: 对任意x∈(0,1)恒有f(x)>f(0)=1.
(ⅱ)当a>2时, 取x
0= ∈(0,1),则由(Ⅰ)知 f(x
0)<f(0)=1
(ⅲ)当a≤0时, 对任意x∈(0,1),恒有 >1且e
-ax≥1,得
f(x)= e
-ax≥ >1. 综上当且仅当a∈(-∞,2]时,对任意x∈(0,1)恒有f(x)>1.

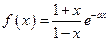 。
。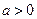 ,讨论
,讨论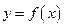 的单调性;
的单调性;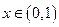 恒有
恒有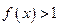 ,求
,求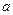 的取值范围。
的取值范围。
