Question

设a，b为两条直线，α，β为两个平面，下列四个命题中，正确的命题是（ ）
A．若a，b与α所成的角相等，则α∥b
B．若a∥α，b∥β，α∥β，则a∥b
C．若a?α，b?β，α∥b，则α∥β
D．若a⊥α，b⊥β，α⊥β，是a⊥b

Answer 1

【答案】分析：根据题意，依次分析选项，A、用直线的位置关系判断．B、用长方体中的线线，线面，面面关系验证．C、用长方体中的线线，线面，面面关系验证．D、由a⊥α，α⊥β，可得到a?β或a∥β，再由b⊥β得到结论．
解答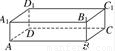：解：A、直线a，b的方向相同时才平行，不正确；
B、用长方体验证．如图，设A₁B₁为a，平面AC为α，BC为b，平面A₁C₁为β，显然有a∥α，b∥β，α∥β，但得不到a∥b，不正确；
C、可设A₁B₁为a，平面AB₁为α，CD为b，平面AC为β，满足选项C的条件却得不到α∥β，不正确；
D、∵a⊥α，α⊥β，
∴a?β或a∥β
又∵b⊥β
∴a⊥b
故选D
点评：本题主要考查空间内两直线，直线与平面，平面与平面间的位置关系，综合性强，方法灵活，属中档题．