
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,左顶点为A,左焦点为F1(﹣2,0),点B(2, ![]() )在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
)在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
(Ⅰ)求椭圆C的方程;
(Ⅱ)在x轴上是否存在点P,使得无论非零实数k怎样变化,总有∠MPN为直角?若存在,求出点P的坐标,若不存在,请说明理由.
【答案】解:(Ⅰ)由题意可设椭圆方程为 ![]() (a>b>0),
(a>b>0),
则c=2,a2﹣b2=c2 , ![]() =1,解得:a2=8,b2=4.
=1,解得:a2=8,b2=4.
可得椭圆C的方程为 ![]() =1;
=1;
(Ⅱ)如图,设F(x0 , y0),E(﹣x0 , ﹣y0),则 ![]() =1,A(﹣2
=1,A(﹣2 ![]() ,0),
,0),
AF所在直线方程y= ![]() (x+2
(x+2 ![]() ),
),
取x=0,得y=  ,
,
∴N(0,  ),
),
AE所在直线方程为y= ![]() (x+2
(x+2 ![]() ),
),
取x=0,得y=  .
.
则以MN为直径的圆的圆心坐标为(0, ![]() ),
),
半径r= ![]() ,
,
圆的方程为x2+(y﹣ ![]() )2=
)2=  =
= ![]() ,即x2+(y+
,即x2+(y+ ![]() )2=
)2= ![]() .
.
取y=0,得x=±2.
可得以MN为直径的圆经过定点(±2,0).
可得在x轴上存在点P(±2,0),
使得无论非零实数k怎样变化,总有∠MPN为直角.
【解析】(Ⅰ)由题意可设椭圆标准方程为 ![]() (a>b>0),结合已知及隐含条件列关于a,b,c的方程组,求解方程组得到a2 , b2的值,则椭圆方程可求;(Ⅱ)设F(x0 , y0),E(﹣x0 , ﹣y0),写出AE、AF所在直线方程,求出M、N的坐标,得到以MN为直径的圆的方程,由圆的方程可知以MN为直径的圆经过定点(±2,0),即可判断存在点P.
(a>b>0),结合已知及隐含条件列关于a,b,c的方程组,求解方程组得到a2 , b2的值,则椭圆方程可求;(Ⅱ)设F(x0 , y0),E(﹣x0 , ﹣y0),写出AE、AF所在直线方程,求出M、N的坐标,得到以MN为直径的圆的方程,由圆的方程可知以MN为直径的圆经过定点(±2,0),即可判断存在点P.


科目:高中数学 来源: 题型:
【题目】已知{an}是首项为a1 , 公比为q的等比数列,Sn是{an}的前n项和.Sn= ![]() ;若am+an=as+at , 则m+n=s+t;Sk , S2k﹣Sk , S3k﹣S2k成等比数列(k∈N).
;若am+an=as+at , 则m+n=s+t;Sk , S2k﹣Sk , S3k﹣S2k成等比数列(k∈N).
以上说法正确的有( )个.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校1200名高三年级学生参加了一次数学测验(满分为100分),为了分析这次数学测验的成绩,从这1200人的数学成绩中随机抽出200人的成绩绘制成如下的统计表,请根据表中提供的信息解决下列问题;
(1)求a、b、c的值;
(2)如果从这1200名学生中随机取一人,试估计这名学生该次数学测验及格的概率p(注:60分及60分以上为及格);
(3)试估计这次数学测验的年级平均分.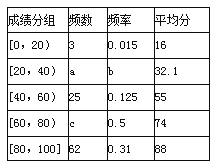
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三文科分为五个班.高三数学测试后,随机地在各班抽取部分学生进行成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了18人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,任取一名学生,求分数不小于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】是否存在过点(﹣5,﹣4)的直线l,使它与两坐标轴围成的三角形的面积为5?若存在,求出直线l的方程(化成直线方程的一般式);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 【2017四川宜宾二诊】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,已知点
中,已知点![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为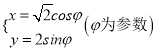 .以原点为极点,
.以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为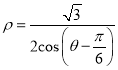 .
.
(Ⅰ)判断点![]() 与直线
与直线![]() 的位置关系并说明理由;
的位置关系并说明理由;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 的两个交点分别为
的两个交点分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC, ![]() .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
(Ⅰ)求证:MN∥平面BDE;
(Ⅱ)求二面角C-EM-N的正弦值;
(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为![]() ,求线段AH的长.
,求线段AH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com