设集合A={x|f(x)=x},B={x|f[f(x)]=x}.
(1)设f(x)=x2-x-3,求集合A与B;
(2)设f(x)=x2-(2a-1)x+a2(常数a∈R),求证:A=B.
(3)猜测集合A与B的关系并给予证明.
解(1)由A={x|f(x)=x},知集合A的元素就是方程f(x)=x的解.
即f(x)=x?x
2-x-3=x?x=-1或x=3.所以A={-1,3}.
同理,集合B的元素就是方程f[f(x)]=x的解
即(x
2-x-3)
2-(x
2-x-3)-3=x?(x
2-x-3)
2-x
2=0.

.所以
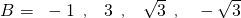
.
(2)由f(x)=x
2-(2a-1)x+a
2,
得方程f(x)-x=(x-a)
2=0的解为x=a,所以A={a};
而方程f[f(x)]=x的解是集合B的元素,
即[f(x)]
2-f(x)=[f(x)-a]
2?[(x-a)
2+x-a]
2+(x-a)
2=0.(x-a)
2[(x-a+1)
2+1]=0?x=a,所以B={a}.
故A=B.
(3)若A=∅,显然A⊆B.
若A≠∅,任取x
0∈A,于是f(x
0)=x
0,
则f[f(x
0)]=f(x
0)=x
0,所以x
0∈B,∴A⊆B.
分析:(1)集合A与B,即方程f(x)=x的解集和方程f[f(x)]=x的解集,分别解方程即可
(2)分别解方程f(x)-x=(x-a)
2=0和[f(x)]
2-f(x)=[f(x)-a]
2?[(x-a)
2+x-a]
2+(x-a)
2=0,即可发现两方程同解
(3)先由(1)(2),猜想A⊆B,再利用子集定义证明对?x
0∈A,都有x
0∈B即可
点评:本题考查了集合的意义,集合间的关系,解题时要熟练掌握一元二次不等式的解法,会运用子集定义证明集合关系

 .所以
.所以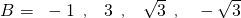 .
.

 设函数f(x)=|x2-2x-8|.
设函数f(x)=|x2-2x-8|. 设函数f(x)=|x2-4x-5|.
设函数f(x)=|x2-4x-5|.