（本小题8分）
观察下列等式：
，
，
，
归纳出一个恒等式，并用数学归纳法证明．
轻松课堂单元期中期末专题冲刺100分系列答案科目：高中数学 来源： 题型：
（本小题满分12分）
某工厂有工人1000名，其中250名工人参加过短期培训（称为A类工人），另外750名工人参加过长期培训（称为B类工人）.现用分层抽样方法（按A类，B类分二层）从该工厂的工人中共抽查100名工人，调查他们的生产能力（生产能力指一天加工的零件数）.
（Ⅰ）A类工人中和B类工人各抽查多少工人？
（Ⅱ）从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1：
| 生产能力分组 |
|
|
|
|
|
| 人数 | 4 | 8 |
| 5 | 3 |
表2：
| 生产能力分组 |
|
|
|
|
| 人数 | 6 | y | 36 | 18 |
（ⅰ）先确定
，再在答题纸上完成下列频率分布直方图。就生产能力而言，A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小？（不用计算，可通过观察直方图直接回答结论）
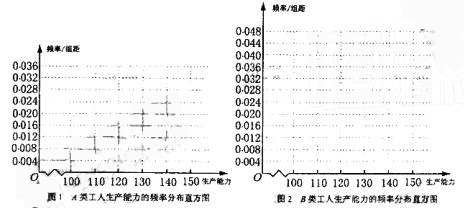
（ii）分别估计
类工人和
类工人生产能力的平均数，并估计该工厂工人和生产能力的平均数（同一组中的数据用该区间的中点值作代表）。
查看答案和解析>>
科目：高中数学 来源：2015届云南省高一上学期期末考试数学试卷（解析版） 题型：解答题
（本小题满分12分）探究函数
的最小值，并确定取得最小值时x的值.列表如下：
|
x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
y |
… |
16 |
10 |
8.34 |
8.1 |
8.01 |
8 |
8.01 |
8.04 |
8.08 |
8.6 |
10 |
11.6 |
15.14 |
… |
请观察表中y值随x值变化的特点，完成以下的问题.
(1)函数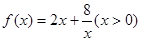
在区间（0，2）上递减；函数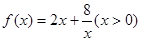在区间 上递增.当
时，
.
(2)证明：函数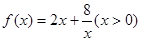在区间（0，2）递减.
(3)思考：函数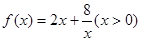时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
查看答案和解析>>
科目：高中数学 来源：2014届福建省高二上学期期中考试文科数学试题（解析版） 题型：解答题
（本小题12分）某工厂有工人1000名，其中250名工人参加过短期培训（称为A类工人），另外750名工人参加过长期培训（称为B类工人）.现用分层抽样方法（按A类，B类分二层）从该工厂的工人中共抽查100名工人，调查他们的生产能力（生产能力指一天加工的零件数）.从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1：
|
生产能力分组 |
|
|
|
|
|
|
人数 |
4 |
8 |
|
5 |
3 |
表2：
|
生产能力分组 |
|
|
|
|
|
人数 |
6 |
y |
36 |
18 |
（1）先确定
，再在答题纸上完成下列频率分布直方图。就生产能力而言，A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小？（不用计算，可通过观察直方图直接回答结论）(注意:本题请在答题卡上作图)
（2）分别估计
类工人和
类工人生产能力的众数、中位数和平均数。（精确到0.1）
查看答案和解析>>
科目：高中数学 来源： 题型：
（本小题16分）
探究函数
的最大值，并确定取得最大值时
的值.列表如下：
|
| … | -0.5 | -1 | -1.5 | -1.7 | -1.9 | -2 | -2.1 | -2.2 | -2.3 | -3 | … |
|
| … | -8.5 | -5 | -4.17 | -4.05 | -4.005 | -4 | -4.005 | -4.02 | -4.04 | -4.3 | … |
请观察表中
值随值变化的特点，完成以下的问题.
（1）函数在区间 上为单调递增函数.当
时，
.
（2）证明：函数
在区间
为单调递减函数.
（3）思考：函数
有最大值或最小值吗？如有，是多少？此时为何值？（直接回答结果，不需证明）.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
． …………………………3分
时，左边
，右边
，
等式成立；………4分
时，等式成立，即
，则
时，左边
右边，
N*，等式恒成立． ………………………8分
