
 表示“B1和C1全被选中”,先求P(
表示“B1和C1全被选中”,先求P( ),再由对立事件的概率公式可得答案.
),再由对立事件的概率公式可得答案.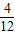 =
=
 表示“B1和C1全被选中”,
表示“B1和C1全被选中”, ={={(A1,B1,C1),(A2,B1,C1),(A3,B1,C1)}共3个基本事件,
={={(A1,B1,C1),(A2,B1,C1),(A3,B1,C1)}共3个基本事件,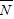 )=
)= =
= ,由对立事件的概率公式可得P(N)=1-P(
,由对立事件的概率公式可得P(N)=1-P( )=1-
)=1- =
=


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西师大附中高二(上)期中数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:新课标高三数学事件与概率、古典概型专项训练(河北) 题型:填空题
现有2008年奥运会志愿者7名,其中4名为男性,3名为女性,从中任选2名志愿者为游客做向导,其中下列事件:
①恰有1名女性与恰有2名女性;
②至少有1名女性与全是女性;
③至少有1名男性与至少有1名女性;
④至少有1名女性与全是男性.
是互斥事件的组数有________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com