
【题目】
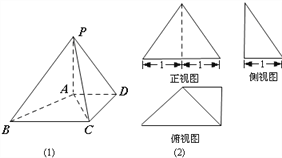
有一个侧面是正三角形的四棱锥![]() 如图(1),它的三视图如图(2).
如图(1),它的三视图如图(2).
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与正三角形侧面所成二面角的余弦值.
与正三角形侧面所成二面角的余弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】试题分析:(Ⅰ)由三视图可知,四棱锥![]() 中
中![]() 平面
平面![]() ,四边形
,四边形![]() 为直角梯形,在底面证出
为直角梯形,在底面证出![]() ,又
,又![]() 即得证.
即得证.
(Ⅱ)由三视图可知,四棱锥![]() 的正三角形侧面为面
的正三角形侧面为面![]() 建立空间直角坐标系,找出两个面的法向量,找向量的夹角的余弦值即得解
建立空间直角坐标系,找出两个面的法向量,找向量的夹角的余弦值即得解
试题解析:
(Ⅰ)由三视图可知,四棱锥![]() 中
中![]() 平面
平面![]() ,
,
同时, ![]() ,四边形
,四边形![]() 为直角梯形.
为直角梯形.
过点![]() 作
作![]() 于
于![]() ,则
,则![]() ,
, ![]() .
.
∴![]() ,
, ![]() ,
,
∴![]() ,故
,故![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)由三视图可知,四棱锥![]() 的正三角形侧面为面
的正三角形侧面为面![]() .
.
![]()
![]() 为正三角形,∴
为正三角形,∴![]() .在
.在![]() 中,
中, ![]() .
.
以![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
有![]() .
.
由(Ⅰ)知![]() 是平面
是平面![]() 的一条法向量.
的一条法向量.
向量![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() ,得
,得![]() 的一组解
的一组解![]() .
.
设平面![]() 与正三角形侧面
与正三角形侧面![]() 所成二面角为
所成二面角为![]() ,则
,则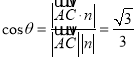


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρ=
(t为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρ= ![]() .
.
(1)写出直线l的极坐标方程与曲线C的普通方程;
(2)若点 P是曲线C上的动点,求 P到直线l的距离的最小值,并求出 P点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①定义在R上的函数f(x)满足f(﹣2)=f(2),则f(x)不是奇函数
②定义在R上的函数f(x)恒满足f(﹣x)=|f(x)|,则f(x)一定是偶函数
③一个函数的解析式为y=x2 , 它的值域为{0,1,4},这样的不同函数共有9个
④设函数f(x)=lnx,则对于定义域中的任意x1 , x2(x1≠x2),恒有 ![]() ,
,
其中为真命题的序号有(填上所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家规定个人稿费纳税办法是:不超过800元的不纳税;超过800元而不超过4 000元的按超过800元部分的14%纳税;超过4 000元的按全部稿酬的11%纳税.已知某人出版一本书,共纳税420元,这个人应得稿费(扣税前)为( )
A.2800元
B.3000元
C.3800元
D.3818元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=2sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个周期后,所得图象对应的函数为( )
个周期后,所得图象对应的函数为( )
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin(2x﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f′(x)是奇函数f(x)(x∈R)的导函数,f(﹣2)=0,当x>0时,xf′(x)﹣f(x)>0,则使得f(x)>0成立的x的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区停车场的收费标准为:每车每次停车时间不超过2小时免费,超过2小时的部分每小时收费1元(不足1小时的部分按1小时计算).现有甲乙两人相互独立到停车场停车(各停车一次),且两人停车的时间均不超过5小时,设甲、乙两人停车时间(小时)与取车概率如下表所示:

(1)求甲、乙两人所付车费相同的概率;
(2)设甲、乙两人所付停车费之和为随机变量![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数 ![]() (m∈Z)的图象关于y轴对称,且在区间(0,+∞)为减函数
(m∈Z)的图象关于y轴对称,且在区间(0,+∞)为减函数
(1)求m的值和函数f(x)的解析式
(2)解关于x的不等式f(x+2)<f(1﹣2x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】⊙O1和⊙O2的极坐标方程分别为ρ=4cosθ,ρ=﹣4sinθ.
(1)⊙O1和⊙O2的极坐标方程化为直角坐标方程;
(2)求经过⊙O1和⊙O2交点的直线的直角坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com