
 53天天练系列答案
53天天练系列答案科目:高中数学 来源:不详 题型:解答题
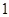 个、黄色球
个、黄色球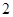 个、蓝色球
个、蓝色球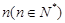 个.现进行从口袋中摸球的游戏:摸到红球得
个.现进行从口袋中摸球的游戏:摸到红球得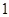 分、摸到黄球得
分、摸到黄球得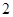 分、摸到蓝球得
分、摸到蓝球得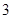 分.若从这个口袋中随机地摸出
分.若从这个口袋中随机地摸出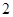 个球,恰有一个是黄色球的概率是
个球,恰有一个是黄色球的概率是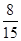 .
.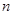 的值;⑵从口袋中随机摸出
的值;⑵从口袋中随机摸出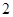 个球,设
个球,设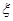 表示所摸
表示所摸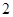 球的得分之和,求
球的得分之和,求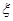 的分布列和数学期望
的分布列和数学期望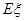 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
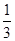 ,
,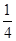 ,3,4中随机抽取一个数记为a,从集合{-1,1,-2,2}中随机抽取一个数记为b,则函数f(x)=ax+b(a>0,a≠1)的图像经过第三象限的概率是________.
,3,4中随机抽取一个数记为a,从集合{-1,1,-2,2}中随机抽取一个数记为b,则函数f(x)=ax+b(a>0,a≠1)的图像经过第三象限的概率是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
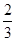 ,则甲以3∶1的比分获胜的概率为( )
,则甲以3∶1的比分获胜的概率为( )A.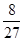 | B.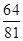 | C.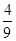 | D.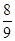 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
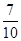 为概率的事件是( )
为概率的事件是( )| A.都不是一等品 | B.恰有1件一等品 |
| C.至少有1件一等品 | D.至多有1件一等品 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
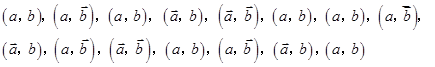
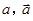 分别表示甲组研发成功和失败;
分别表示甲组研发成功和失败;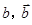 分别表示乙组研发成功和失败.
分别表示乙组研发成功和失败.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B.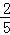 | C.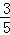 | D.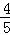 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com