
如图,已知正三棱锥A―BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.

(1)求此正三棱锥的高;
(2)求二面角E―FD―B的大小.
解法一:(1)由正三棱锥的性质知AC⊥BD.
EF//AC,
∴EF⊥BD.又EF⊥ED.故EF⊥平面ABD,即
AC⊥平面ABD,∴AC⊥AB,AC⊥AD.
又∵A―BCD为正三棱锥,
∴AB⊥AD,
从而AB=AC=AD=![]() ?BC=
?BC=![]() .
.
设△BCD中心为O,则棱锥高为
AO=![]() .
.
(2)过E作EH⊥BO于H,则EH∥AO,即EH⊥平面BCD.
又过H作HG⊥DF于G,连EG,则EG⊥DF,
故∠HGE为二面角E一FD一B的平面角.
∵EH=![]() AO=
AO=![]() ,HG=
,HG=![]() BF=
BF=![]() ,
,
∴tan∠EGH=![]() =
=![]() ×2=
×2=![]() ,
,
∠EGH=arctan![]()
解法二:(1)建立如图所示的空间直角坐标系,
则B、C、D的坐标为B(0,0,0),C(![]() ,1,0),D(0,2,0),
,1,0),D(0,2,0),
若设棱锥高为h,又A在平面BCD上的射影为ABCD的中心,
则A的坐标为(![]() ,1,h).
,1,h).

∵E、F为AB、BC的中点,
∴E(![]() ,
,![]() ,h),F(
,h),F(![]() ,
,![]() ,0).
,0).
∵EF⊥DE,∴![]() ,
,
即(![]() ,0,一
,0,一![]() )?(
)?(![]() ,一
,一![]() ,一
,一![]() )=0
)=0
∴![]() ,
,![]() .
.
(2)设m=(![]() ,
,![]() ,z)为平面DEF的法向量,则
,z)为平面DEF的法向量,则
 .即
.即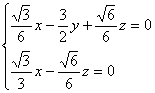
令z=1,则![]()
又平面BCD的法向量n=(0,0,1),由m,n的方向知,当二面角E―FD―B设为![]() 时,
时,
cos![]() =
=![]() ,
,![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
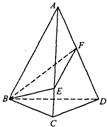 如图,已知正三棱锥A-BCD侧面的顶角为40°,侧棱长为a,动点E、F分别在侧棱AC、AD上,则以线段BE、EF、FB长度和的最小值为半径的球的体积为( )
如图,已知正三棱锥A-BCD侧面的顶角为40°,侧棱长为a,动点E、F分别在侧棱AC、AD上,则以线段BE、EF、FB长度和的最小值为半径的球的体积为( )A、4
| ||
B、
| ||
C、
| ||
| D、4πa3 |
查看答案和解析>>
科目:高中数学 来源:2009年辽宁省大连市高考数学一模试卷(理科)(解析版) 题型:选择题



查看答案和解析>>
科目:高中数学 来源:2012年高考数学预测试卷3(理科)(解析版) 题型:选择题




查看答案和解析>>
科目:高中数学 来源:2012年高考数学预测试卷3(文科)(解析版) 题型:选择题




查看答案和解析>>
科目:高中数学 来源:2009-2010学年辽宁省沈阳市东北育才学校高三(下)3月月考数学试卷(理科)(解析版) 题型:选择题




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com