
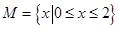 ,
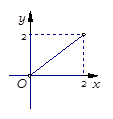
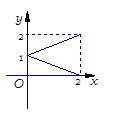
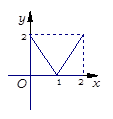
,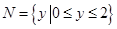 ,给出如下四个图形,其中能表
,给出如下四个图形,其中能表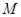 到集合
到集合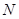 的函数关系的是 ( )
的函数关系的是 ( )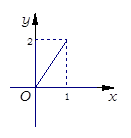


科目:高中数学 来源:不详 题型:解答题
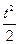 (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
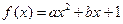 (
(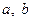 为实数,
为实数,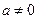 ,
,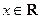 ),
),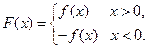
 ,且函数
,且函数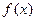 的值域为
的值域为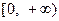 ,求
,求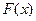 的表达式;
的表达式;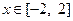 时,
时,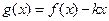 是单调函数,求实数
是单调函数,求实数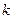 的取值范围;
的取值范围;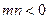 ,
,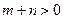 ,
,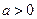 ,且函数
,且函数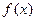 为偶函数,判断
为偶函数,判断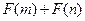 是否大于
是否大于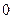 ?
?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
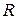 上的偶函数
上的偶函数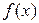 满足:
满足: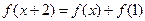 且在区间
且在区间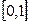 上
上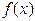 性质的表述:
性质的表述: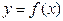 的图象关于直线
的图象关于直线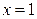 对称; ②函数
对称; ②函数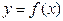 是周期函数;
是周期函数;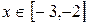 时,
时,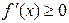 ; ④函数
; ④函数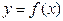 的图象上横坐标为偶数的点都是函数的极小值点。 其中正确表述的番号是 .
的图象上横坐标为偶数的点都是函数的极小值点。 其中正确表述的番号是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com