
| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | $-\frac{{\sqrt{5}}}{3}$ | D. | $\frac{{\sqrt{5}}}{3}$ |
分析 根据题意画出图形,结合图形得出AB为截面圆的直径,求出AB的值以及三棱柱外接球的半径R;再利用三角形以及空间向量的知识求出向量$\overrightarrow{{AC}_{1}}$与$\overrightarrow{{B}_{1}C}$夹角的余弦值的绝对值即可.
解答 解:∵∠BCA=90°,BC=CA=2,
∴AB=2$\sqrt{2}$,且为截面圆的直径;
又三棱柱外接球的体积为$\frac{32π}{3}$,
∴$\frac{4}{3}$π•R3=$\frac{32π}{3}$,
解得外接球的半径为R=2;
△ABC1中,AB⊥BC1,AB=2$\sqrt{2}$,AC1=2R=4,
∴BC1=$\sqrt{{4}^{2}{-(2\sqrt{2})}^{2}}$=2$\sqrt{2}$;
又$\overrightarrow{{AC}_{1}}$=$\overrightarrow{AC}$+$\overrightarrow{{CC}_{1}}$,$\overrightarrow{{B}_{1}C}$=$\overrightarrow{{B}_{1}B}$+$\overrightarrow{BC}$=-$\overrightarrow{{CC}_{1}}$-$\overrightarrow{CB}$,
∴$\overrightarrow{{AC}_{1}}$•$\overrightarrow{{B}_{1}C}$=$\overrightarrow{AC}$•(-$\overrightarrow{{CC}_{1}}$)-$\overrightarrow{AC}$•$\overrightarrow{AB}$-${\overrightarrow{{CC}_{1}}}^{2}$-$\overrightarrow{{CC}_{1}}$•$\overrightarrow{CB}$
=0-0-${(2\sqrt{2})}^{2}$-0
=-8,
|$\overrightarrow{{AC}_{1}}$|=|$\overrightarrow{{B}_{1}C}$|=$\sqrt{{(2\sqrt{2})}^{2}{+2}^{2}}$=$\sqrt{12}$;
∴异面直线B1C与AC1所成的角θ的余弦值为:
cosθ=|$\frac{\overrightarrow{{AC}_{1}}•\overrightarrow{{B}_{1}C}}{|\overrightarrow{{AC}_{1}}|×|\overrightarrow{{B}_{1}C}|}$|=|$\frac{-8}{\sqrt{12}×\sqrt{12}}$|=$\frac{2}{3}$.
故选:B.
点评 本题考查了异面直线所成角的计算问题,解题时可以利用两向量所成的角进行计算,是综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
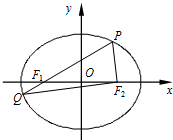 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设$\overrightarrow{P{F}_{1}}$=λ$\overrightarrow{{F}_{1}Q}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设$\overrightarrow{P{F}_{1}}$=λ$\overrightarrow{{F}_{1}Q}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3<x<2 | B. | -2<x<3 | C. | -5<x<1 | D. | -1<x<5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com