
【题目】已知函数 ![]() .
.
(I)若α是第二象限角,且 ![]() 的值;
的值;
(Ⅱ)求函数f(x)在[0,2π]上的单调递增区间.
【答案】解:(I)α是第二象限角,且 ![]() ,
,
则: ![]() ,
,
解得: ![]() ,
,
α是第二象限角,
解得: ![]() ,
, ![]() ,
,
所以 ![]() ,
,
= ![]() .
.
= ![]() ,
,
= ![]() .
.
(Ⅱ)由题意得: ![]() ,
,
= ![]() ,
,
= ![]() ,
,
= ![]() ,
,
令 ![]() ,
,
解得: ![]() ,
,
由于:0≤x≤2π,则:
①当k=0时,函数的单调递增区间为:[0, ![]() ],
],
②当k=1时,函数的单调递增区间为:[ ![]() ],
],
③当k=2时,函数的单调递增区间为:[ ![]() ].
].
故函数的单调递增区间为::[0, ![]() ]和[
]和[ ![]() ]和[
]和[ ![]() ]
]
【解析】(1)根据tan![]() =
=![]() 将tan
将tan![]() 用sin
用sin![]() 、cos
、cos![]() 表示,又因为sin2
表示,又因为sin2![]() +cos2
+cos2![]() =1,求出sin
=1,求出sin![]() 、coa
、coa![]() ;(2)根据两角差的余弦公式、二倍角的正余弦公式及辅助角公式将f(x)转化成y=Asin(
;(2)根据两角差的余弦公式、二倍角的正余弦公式及辅助角公式将f(x)转化成y=Asin(![]() )的形式,令-
)的形式,令-![]() +k
+k![]()
![]()
![]()
![]()
![]() +k
+k![]() (k
(k![]() z),解出x后给k赋值,找到符合条件的区间.
z),解出x后给k赋值,找到符合条件的区间.
【考点精析】解答此题的关键在于理解同角三角函数基本关系的运用的相关知识,掌握同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣a)(x﹣b)(x﹣c)(其中a>1,b>1),x=0是f(x)的一个零点,曲线y=f(x)在点(1,f(1))处的切线平行于x轴,则a+b的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商计划经营一种商品,经市场调查发现,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克,1<x≤12)满足:当1<x≤4时,y=a(x﹣3)2+ ![]() ,(a,b为常数);当4<x≤12时,y=
,(a,b为常数);当4<x≤12时,y= ![]() ﹣100.已知当销售价格为2元/千克时,每日可售出该特产800千克;当销售价格为3元/千克时,每日可售出150千克.
﹣100.已知当销售价格为2元/千克时,每日可售出该特产800千克;当销售价格为3元/千克时,每日可售出150千克.
(1)求a,b的值,并确定y关于x的函数解析式;
(2)若该商品的销售成本为1元/千克,试确定销售价格x的值,使店铺每日销售该特产所获利润f(x)最大.( ![]() ≈2.65)
≈2.65)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π]),OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论,其中不正确的是( )
①f( ![]() )=
)= ![]()
②函数f(x)在( ![]() ,π)上为减函数
,π)上为减函数
③任意x∈[0, ![]() ],都有f(x)+f(π﹣x)=4.
],都有f(x)+f(π﹣x)=4.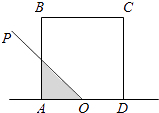
A.①
B.③
C.②
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女子善织,日益功,疾,初日织五尺,今一月织九匹三丈(1匹=40尺,一丈=10尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织5尺,一月织了九匹三丈,问每天增加多少尺布?”若一个月按31天算,记该女子一个月中的第n天所织布的尺数为an , 则 ![]() 的值为( )
的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sinωx,1),
sinωx,1), ![]() =(cosωx,cos2ωx+1),设函数f(x)=
=(cosωx,cos2ωx+1),设函数f(x)= ![]() .
.
(1)若函数f(x)的图象关于直线x= ![]() 对称,且ω∈[0,3]时,求函数f(x)的单调增区间;
对称,且ω∈[0,3]时,求函数f(x)的单调增区间;
(2)在(1)的条件下,当 ![]() 时,函数f(x)有且只有一个零点,求实数b的取值范围.
时,函数f(x)有且只有一个零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示: 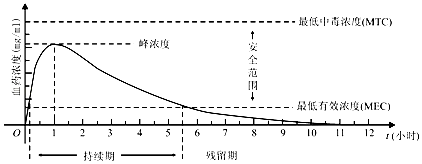
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的是( )
A.首次服用该药物1单位约10分钟后,药物发挥治疗作用
B.每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
C.每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
D.首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:mx2+ny2=1,(m>0,n<0)的一条渐近线与圆x2+y2﹣6x﹣2y+9=0相切,则双曲线C的离心率等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com