
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女子善织,日益功,疾,初日织五尺,今一月织九匹三丈(1匹=40尺,一丈=10尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织5尺,一月织了九匹三丈,问每天增加多少尺布?”若一个月按31天算,记该女子一个月中的第n天所织布的尺数为an , 则 ![]() 的值为( )
的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=x+ ![]() (x>0)都在x=x0处取得最小值.
(x>0)都在x=x0处取得最小值.
(1)求f(x0)﹣g(x0)的值.
(2)设函数h(x)=f(x)﹣g(x),h(x)的极值点之和落在区间(k,k+1),k∈N,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1(﹣1,0),F2(1,0)分别是椭圆C: ![]() =1(a>0)的左、右焦点.
=1(a>0)的左、右焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若A,B分别在直线x=﹣2和x=2上,且AF1⊥BF1 .
(ⅰ)当△ABF1为等腰三角形时,求△ABF1的面积;
(ⅱ)求点F1 , F2到直线AB距离之和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A、B、C的对边分别为a,b,c,已知A≠ ![]() ,且3sinAcosB+
,且3sinAcosB+ ![]() bsin2A=3sinC.
bsin2A=3sinC.
(I)求a的值;
(Ⅱ)若A= ![]() ,求△ABC周长的最大值.
,求△ABC周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(cosx)﹣x与函数g(x)=cos(sinx)﹣x在区间 ![]() 内都为减函数,设
内都为减函数,设 ![]() ,且cosx1=x1 , sin(cosx2)=x2 , cos(sinx3)=x3 , 则x1 , x2 , x3的大小关系是( )
,且cosx1=x1 , sin(cosx2)=x2 , cos(sinx3)=x3 , 则x1 , x2 , x3的大小关系是( )
A.x1<x2<x3
B.x3<x1<x2
C.x2<x1<x3
D.x2<x3<x1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PD⊥平面PAB,AD∥BC,BC=CD= ![]() AD,E,F分别为线段AD,PD的中点.
AD,E,F分别为线段AD,PD的中点. 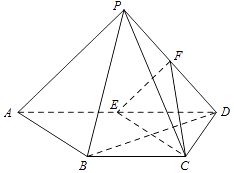
(Ⅰ)求证:CE∥平面PAB;
(Ⅱ)求证:PD⊥平面CEF;
(Ⅲ)写出三棱锥D﹣CEF与三棱锥P﹣ABD的体积之比.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2 ![]() ,且AC,BD交于点O,E是PB上任意一点.
,且AC,BD交于点O,E是PB上任意一点.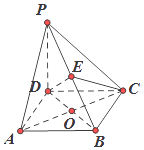
(1)求证:AC⊥DE
(2)已知二面角A﹣PB﹣D的余弦值为 ![]() ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com