
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元,根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足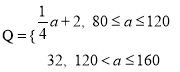 ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当投资甲城市128万元时,求此时公司总收益;
⑵试问如何安排甲、乙两个城市的投资,才能使公司总收益最大?
【答案】(1)88万元;(2)当甲城市投资128万元,乙城市投资112万元时,总收益最大.
【解析】【试题分析】(1)当甲![]() 万时,乙
万时,乙![]() 万,代入收益表达式可求得投资收益.(2)设投资甲
万,代入收益表达式可求得投资收益.(2)设投资甲![]() 万,则投资乙
万,则投资乙![]() 万.对
万.对![]() 分成
分成![]() ,
, ![]() 两种情况,求出总收益的表达式,利用一次函数和二次函数最值求法求得最大值.
两种情况,求出总收益的表达式,利用一次函数和二次函数最值求法求得最大值.
【试题解析】
(1)当![]() 时,此时甲城市投资128万元,乙城市投资112万元
时,此时甲城市投资128万元,乙城市投资112万元
所以总收益![]() (万元)
(万元)
答:总收益为88万元.
(2)由题知,甲城市投资![]() 万元,乙城市投资
万元,乙城市投资![]() 万元
万元
依题意得![]() ,解得
,解得![]()
当![]() 时,
时, ![]()
![]() <
<![]()
当![]() 时,
时, ![]()
![]()
![]()
令![]() ,则
,则![]()
所以![]()
当![]() ,即
,即![]() 万元时,
万元时, ![]() 的最大值为
的最大值为![]()
因为![]()
故![]() 的最大值为
的最大值为![]() (万元)
(万元)
答:当甲城市投资128万元,乙城市投资112万元时,总收益最大,且最大收益为88万元


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
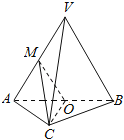
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆 ![]() =1交于抛物线右侧的点B,F为抛物线的焦点,则|AF|+|BF|+|AB|的最大值为( )
=1交于抛物线右侧的点B,F为抛物线的焦点,则|AF|+|BF|+|AB|的最大值为( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥E﹣ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC.
(Ⅰ)证明:平面ABE⊥平面BCE;
(Ⅱ)求二面角A﹣DE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
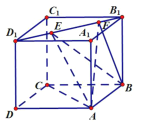
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,则下列结论中正确的是__________.
,则下列结论中正确的是__________.
①![]() 平面
平面![]() ;
;
②平面![]() 平面
平面![]() ;
;
③三棱锥![]() 的体积为定值;
的体积为定值;
④存在某个位置使得异面直线![]() 与
与![]() 成角
成角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1曰8日,中共中央、国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值![]() 与这种新材料的含量
与这种新材料的含量![]() (单位:克)的关系为:当
(单位:克)的关系为:当![]() 时,
时, ![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时, ![]() .测得数据如表(部分)
.测得数据如表(部分)
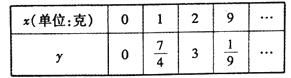
(1)求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)其函数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx,若存在x1 , x2 , ,xm满足0≤x1<x2<xm≤6π,且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+|f(xn﹣1)﹣f(xn)|=12,(m≥2,m∈N*),则m的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com