
| 2 |
| 3 |
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
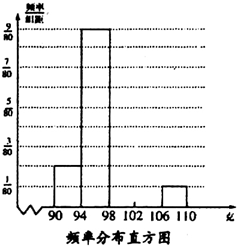 为了解食品厂生产的一种食品中添加剂的含量,食品监管部门随机抽取了一个批次的20袋样品进行检验,获得以下频率分布表和频率分布直方图:
为了解食品厂生产的一种食品中添加剂的含量,食品监管部门随机抽取了一个批次的20袋样品进行检验,获得以下频率分布表和频率分布直方图:| 添加剂(单位克) | 频数 |
| [90,94) | 2 |
| [94,98) | a |
| [98,102) | B |
| [102,106) | 3 |
| [106,110) | 1 |
| 合计 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:
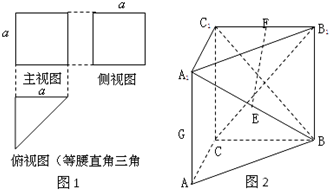 一个三棱柱的三视图及直观图如图所示,E,F,G分别是A1B,B1C1,AA1的中点,AA1⊥底面ABC.
一个三棱柱的三视图及直观图如图所示,E,F,G分别是A1B,B1C1,AA1的中点,AA1⊥底面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| a |
| OB |
| b |
| OP |
| p |
| a |
| b |
| p |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3a2 |
| p |
| 2b2 |
| p |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com