

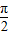 ],上的值域为[0,3],求出a,b即可得到f(x)的解析式.
],上的值域为[0,3],求出a,b即可得到f(x)的解析式.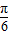 )-4acos2x+3a+b
)-4acos2x+3a+b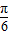 )-cos2x)+a+b
)-cos2x)+a+b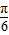 )+a+b.
)+a+b.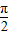 ],
],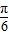 ∈[-
∈[-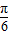 ,
,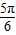 ].∴sin(2x-
].∴sin(2x-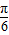 )∈[-
)∈[- ,1].
,1].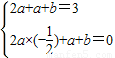 ⇒
⇒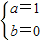 ⇒f(x)=2sin(2x-
⇒f(x)=2sin(2x- )+1.
)+1.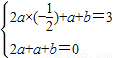 ⇒
⇒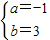 ⇒f(x)=-2sin(2x-
⇒f(x)=-2sin(2x-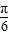 )+2.
)+2.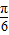 )+2.
)+2.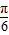 -=kπ⇒x=
-=kπ⇒x=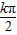 +
+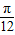 .k∈Z.
.k∈Z.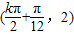 (k∈Z)
(k∈Z)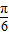 )+1,
)+1,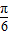 个单位得到:y=2sin(x-
个单位得到:y=2sin(x- ),再各点纵坐标不变,横坐标缩短为原来的
),再各点纵坐标不变,横坐标缩短为原来的 倍得到:y=2sin(2x-
倍得到:y=2sin(2x-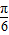 ),再整体向上平移1个单位即可得到:y=2sin(2x-
),再整体向上平移1个单位即可得到:y=2sin(2x-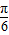 )+1.
)+1.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
| x | x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2-(a+3)x+2a+3 | f(x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com