
【题目】(2015·江苏)如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1 , 设AB1的中点为D,B1CB![]() C1=E.求证:
C1=E.求证:
(1)DE∥平面AA1C1C
(2)BC1⊥AB1
【答案】
(1)
见解析。
(2)
见解析。
【解析】由三棱锥性质知侧面BB1C1C为平行四边形,因此点E为B1C的中点,从而由三角形中位线性质得DE∥AC,,再由线面平行判定定理得DE∥平面AA1C1C(2)因为直三棱柱ABC-A1B1C1中,BC=CC1所以侧面BB1C1C为正方形,因此BC1⊥B1C,又,AC⊥BC, AC⊥CC1(可由直三棱柱推导),因此由线面垂直判定定理得AC⊥平面BB1C1C,从而AC⊥BC1 , 再由线面垂直判定定理得BC1⊥平面AB1C, 进而可得BC1⊥AB1.
(1)由题意知,E为B1C的中点,又D为A1B的中点,因此DE∥AC。 又因为DE平面AA1C1C, AC![]() 平面AA1C1C,所以DE∥平面AA1C1C。
平面AA1C1C,所以DE∥平面AA1C1C。
(2)因为棱柱ABC-A1B1C1是直三棱柱, 所以CC1⊥平面ABC, 所以AC⊥CC1,又因为AC⊥BC, CC1![]() 平面BCC1B1 , BC
平面BCC1B1 , BC![]() BCC1B1, BC
BCC1B1, BC![]() CC1=C,
CC1=C,
所以AC⊥平面BCC1B1 , 又因为BC1![]() BCC1B1, 所以BC1⊥B1C.
BCC1B1, 所以BC1⊥B1C.
因为AC, B1C![]() 平面B1AC, AC
平面B1AC, AC![]() 1C=C, 所以BC1⊥平面B1AC。 又因为AB1
1C=C, 所以BC1⊥平面B1AC。 又因为AB1![]() 平面B1AC, 所以BC1⊥AB1。
平面B1AC, 所以BC1⊥AB1。
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】![]() 已知f(x)=lnx+a(1-x),问:(1)讨论f(x) 的单调性;(2)当 f(x)有最大值,且最大值大于2a-2 时,求a的取值范围.
已知f(x)=lnx+a(1-x),问:(1)讨论f(x) 的单调性;(2)当 f(x)有最大值,且最大值大于2a-2 时,求a的取值范围.
(1)(I)讨论f(x) 的单调性;
(2)(II)当 f(x)有最大值,且最大值大于2a-2 时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)如图,椭圆E:![]() 的离心率是
的离心率是![]() ,点P(0,1)在短轴CD上, 且
,点P(0,1)在短轴CD上, 且![]() .
.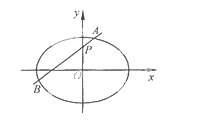
(1)求椭圆E的方程;
(2)设O为坐标原点,过点P的动直线与椭圆交于A、B两点.是否存在常数λ , 使得![]() 为定值?若存在,求λ的值;若不存在,请说明理由.
为定值?若存在,求λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)设fn(x)=x+x2+x...+xn-1, n![]() N, n≥2。
N, n≥2。
(1)fn'(2)
(2)证明:fn(x)在(0,![]() )内有且仅有一个零点(记为an), 且0<an-
)内有且仅有一个零点(记为an), 且0<an-![]() <
<![]() (
(![]() )n.
)n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图,椭圆E:![]() (a>b>0)经过点A(0,-1),且离心率为
(a>b>0)经过点A(0,-1),且离心率为![]() .
.
(1)求椭圆E的方程;
(2)经过点(1,1),且斜率为k的直线与椭圆E交于不同两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)如图I所示
若将运动员按成绩由好到差编为1~35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() ,m 是两条不同的直线,m 垂直于平面
,m 是两条不同的直线,m 垂直于平面![]() ,则“
,则“![]() ”是“
”是“![]() " 的 ( )
" 的 ( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分15分)某工厂某种航空产品的年固定成本为![]() 万元,每生产
万元,每生产![]() 件,需另投入成本为
件,需另投入成本为![]() ,当年产量不足
,当年产量不足![]() 件时,
件时,![]() (万元).当年产量不小于
(万元).当年产量不小于![]() 件时,
件时,![]() (万元).每件商品售价为
(万元).每件商品售价为![]() 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
在如图所示的阳马P-ABCD中,侧棱PD![]() 底面ABCD,且PD=CD,点E是BC的中点,连接DE,BD,BE
底面ABCD,且PD=CD,点E是BC的中点,连接DE,BD,BE
(I)证明:DE![]() 底面PBC,试判断四面体EBCD是否为鳖臑. 若是,写出其四个面的直角(只需写出结论);若不是,请说明理由;
底面PBC,试判断四面体EBCD是否为鳖臑. 若是,写出其四个面的直角(只需写出结论);若不是,请说明理由;
(Ⅱ)记阳马![]() 的体积为
的体积为![]() ,四面体
,四面体![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.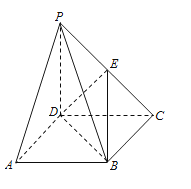
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com