
 ,
, 与
与 平行时,求x的值;
平行时,求x的值; 与
与 夹角为锐角时,求x的范围.
夹角为锐角时,求x的范围.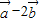 与
与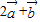 的坐标,再由向量共线的条件建立坐标的方程,求出x的值;
的坐标,再由向量共线的条件建立坐标的方程,求出x的值;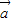 与
与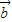 夹角为锐角,则两向量的内积大于0,由于两向量共线同向时,向量的内积也为正,问题应转化为内积为正,且不共线.根据相关公式建立方程求解即可.
夹角为锐角,则两向量的内积大于0,由于两向量共线同向时,向量的内积也为正,问题应转化为内积为正,且不共线.根据相关公式建立方程求解即可.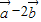 =(2-2x,-1)(2分)
=(2-2x,-1)(2分)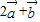 =(4+x,8)(4分)
=(4+x,8)(4分)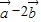 与
与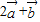 平行得:(2-2x)•8-(-1)•(4+x)=0(6分)
平行得:(2-2x)•8-(-1)•(4+x)=0(6分)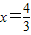 (7分)
(7分)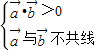 (10分)
(10分)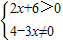 (12分)
(12分)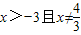 (14分)
(14分)

科目:高中数学 来源:2010-2011学年江苏省盐城市高三年级第三次调研考试数学试卷 题型:解答题
已知函数
(1)当a=0时,求与直线x-y-10 =0平行,且与曲线y=f(x)相切的直线的方程;
(2)求函数 的单调递减区间;
的单调递减区间;
(3)如果存在 ,使函数
,使函数 在x=-3处取得最大值,试求b的最大值。
在x=-3处取得最大值,试求b的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
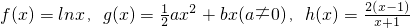
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com