【题目】在等比数列{an}中，前7项和S7=16，又a12+a22+…+a72=128，则a1﹣a2+a3﹣a4+a5﹣a6+a7=（ ）
A.8
B.
C.6
D.
【答案】A
【解析】解答：∵S7=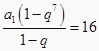 
， ∴a12+a22+…+a72= 
= 
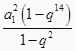=128，
即 
则a1﹣a2+a3﹣a4+a5﹣a6+a7=（a1﹣a2）+（a3﹣a4）+（a5﹣a6）+a7
=a1（1﹣q）+a1q2（1﹣q）+a1q4（1﹣q）+a1q6= 
+a1q6
= 
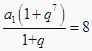；故选A
分析：把已知的前7项和S7=16利用等比数列的求和公式化简，由数列{an2}是首项为a1 ， 公比为q2的等比数列，故利用等比数列的求和公式化简a12+a22+…+a72=128，变形后把第一个等式的化简结果代入求出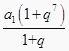 
的值，最后把所求式子先利用等比数列的通项公式化简，把前六项两两结合后，发现前三项为等比数列，故用等比数列的求和公式化简，与最后一项合并后，将求出 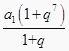的值代入即可求出值．
科目：高中数学 来源： 题型：
【题目】设{an}是等比数列，则下列结论中正确的是（ ）
A. 若a1=1，a5=4，则a3=﹣2
B. 若a1+a3＞0，则a2+a4＞0
C. 若a2＞a1，则a3＞a2
D. 若a2＞a1＞0，则a1+a3＞2a2
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设 
，记不超过x的最大整数为 
，令 
，则 
， 
， 
（ ）
A.是等差数列但不是等比数列
B.是等比数列但不是等差数列
C.既是等差数列又是等比数列
D.既不是等差数列也不是等比数列
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知P是直线
上的动点，过点P作圆
的两条切线，A，B是切点，C是圆心，若四边形PACB面积的最小值为2
，则
的值为( )
A. 3 B. 2 C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知{an}为等差数列，a1+a3+a5=105，a2+a4+a6=99，以Sn表示{an}的前n项和，则使得Sn达到最大值的n是（ ）
A.21
B.20
C.19
D.18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
