
已知函数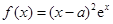 在
在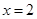 时取得极小值.
时取得极小值.
(1)求实数 的值;
的值;
(2)是否存在区间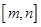 ,使得
,使得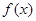 在该区间上的值域为
在该区间上的值域为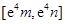 ?若存在,求出
?若存在,求出 ,
,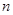 的值;
的值;
若不存在,说明理由.
(1)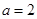 ,(2)满足条件的
,(2)满足条件的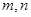 值只有一组,且
值只有一组,且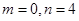 .
.
解析试题分析:(1)根据函数极值求参数,不要忘记列表检验.因为导数为零的点不一定是极值点. 因为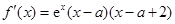 ,所以由题意
,所以由题意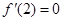 ,解得
,解得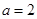 或
或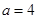 .当
.当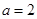 时,
时,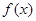 在
在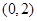 上为减函数,在
上为减函数,在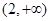 上为增函数,符合题意;当
上为增函数,符合题意;当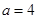 时,
时,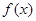 在
在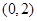 上为增函数,在
上为增函数,在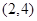 ,
,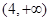 上为减函数,不符合题意.(2)由值域范围确定解析式中参数范围,是函数中难点.主要用到分类讨论的思想方法.首先因为
上为减函数,不符合题意.(2)由值域范围确定解析式中参数范围,是函数中难点.主要用到分类讨论的思想方法.首先因为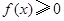 ,所以
,所以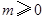 .① 若
.① 若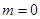 ,则
,则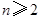 ,因为
,因为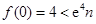 ,所以
,所以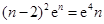 .设
.设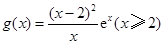 ,则
,则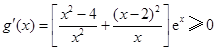 ,所以
,所以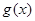 在
在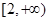 上为增函数.由于
上为增函数.由于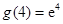 ,即方程
,即方程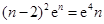 有唯一解为
有唯一解为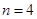 .② 若
.② 若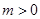 ,则
,则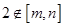 ,即
,即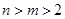 或
或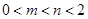 .
.
(Ⅰ)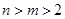 时,
时,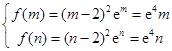 ,由①可知不存在满足条件的
,由①可知不存在满足条件的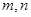 .(Ⅱ)
.(Ⅱ)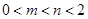 时,
时, ,两式相除得
,两式相除得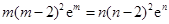 .设
.设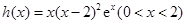 ,则
,则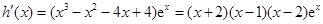 ,
,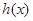 在
在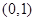 递增,在
递增,在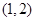 递减,由
递减,由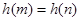 得
得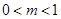 ,
, ,此时
,此时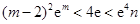 ,矛盾.
,矛盾.
【解】(1)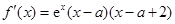 ,
,
由题意知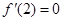 ,解得
,解得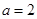 或
或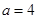 . 2分
. 2分
当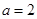 时,
时,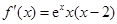 ,
,
易知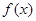 在
在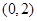 上为减函数,在
上为减函数,在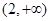 上为增函数,符合题意;
上为增函数,符合题意;
当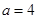 时,
时,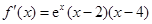 ,
,
易知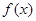 在
在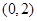 上为增函数,在
上为增函数,在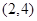 ,
,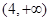 上为减函数,不符合题意.
上为减函数,不符合题意.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知函数 ,
,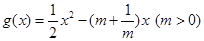 ,且
,且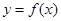 在点
在点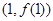 处的切线方程为
处的切线方程为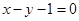 .
.
(1)求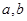 的值;
的值;
(2)若函数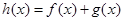 在区间
在区间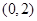 内有且仅有一个极值点,求
内有且仅有一个极值点,求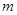 的取值范围;
的取值范围;
(3)设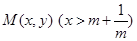 为两曲线
为两曲线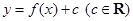 ,
,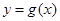 的交点,且两曲线在交点
的交点,且两曲线在交点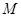 处的切线分别为
处的切线分别为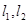 .若取
.若取 ,试判断当直线
,试判断当直线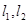 与
与 轴围成等腰三角形时
轴围成等腰三角形时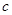 值的个数并说明理由.
值的个数并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数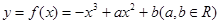
(1)若函数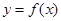 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;
(2)设函数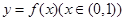 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求 的充要条件;
的充要条件;
(3)若函数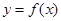 的图象上任意不同的两点的连线的斜率小于l,求证
的图象上任意不同的两点的连线的斜率小于l,求证 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某水产养殖场拟造一个无盖的长方体水产养殖网箱,为了避免混养,箱中要安装一些筛网,其平面图如下,如果网箱四周网衣(图中实线部分)建造单价为每米56元,筛网(图中虚线部分)的建造单价为每米48元,网箱底面面积为160平方米,建造单价为每平方米50元,网衣及筛网的厚度忽略不计.
(1)把建造网箱的总造价y(元)表示为网箱的长x(米)的函数,并求出最低造价;
(2)若要求网箱的长不超过15米,宽不超过12米,则当网箱的长和宽各为多少米时,可使总造价最低?(结果精确到0.01米)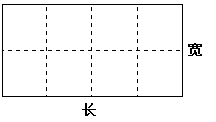
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据统计资料,某工艺品厂的日产量最多不超过20件,每日产品废品率 与日产量
与日产量 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率
(日产品废品率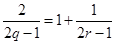
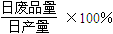 ).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润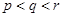 日正品赢利额
日正品赢利额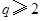 日废品亏损额)
日废品亏损额)
(1)将该车间日利润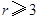 (千元)表示为日产量
(千元)表示为日产量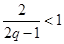 (件)的函数;
(件)的函数;
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=lnx-mx(m R).
R).
(1)若曲线y=f(x)过点P(1,-1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1,x2,求证:x1x2>e2.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数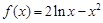
(1)若方程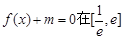 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
(2)如果函数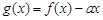 的图象与x轴交于两点
的图象与x轴交于两点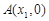 、
、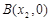 且
且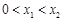 .求证:
.求证: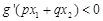 (其中正常数
(其中正常数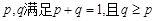 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com