
【题目】在四棱锥P﹣ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC与平面ABCD所成角为45° 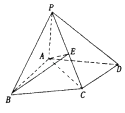
(1)若E为PC的中点,求证:PD⊥平面ABE;
(2)若CD= ![]() ,求点B到平面PCD的距离.
,求点B到平面PCD的距离.
【答案】
(1)证明:∵PA⊥平面ABCD,CD平面ABCD,∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC,而AE平面PAC,∴CD⊥AE.
∵PC与平面ABCD所成角为45°
∴AC=PA,
∵E是PC的中点,∴AE⊥PC,又PC∩CD=C,∴AE⊥平面PCD,
而PD平面PCD,∴AE⊥PD.
∵PA⊥底面ABCD,∴平面PAD⊥平面ABCD,又AB⊥AD,
由面面垂直的性质定理可得BA⊥平面PAD,AB⊥PD,
又AB∩AE=A,∴PD⊥平面ABE.
(2)解:CD= ![]() ,可得AC=3,
,可得AC=3,
∵PA⊥平面ABCD,∴PA⊥AC,∴PC=3 ![]() ,
,
由(1)的证明知,CD⊥平面PAC,∴CD⊥PC,
∵AB⊥AD,△ABC为正三角形,∴∠CAD=30°,
∵AC⊥CD,∴CD=ACtan30°= ![]() .
.
设点B的平面PCD的距离为d,则VB﹣PCD= ![]() ×
× ![]() ×3
×3 ![]() ×
× ![]() ×d=
×d= ![]() d.
d.
在△BCD中,∠BCD=150°,∴S△BCD= ![]() ×3×
×3× ![]() sin150°=
sin150°= ![]() .
.
∴VP﹣BCD= ![]() ×
× ![]() ×3=
×3= ![]() ,
,
∵VB﹣PCD=VP﹣BCD,∴ ![]() d=
d= ![]() ,解得d=
,解得d= ![]() ,
,
即点B到平面PCD的距离为 ![]() .
.
【解析】(1)利用线面垂直的判定与性质定理可得CD⊥平面PAC,CD⊥AE.利用等腰三角形的性质与线面垂直的判定定理可得:AE⊥平面PCD,可得AE⊥PD.利用面面垂直的性质定理与线面垂直的判定定理可得AB⊥PD,进而证明结论.(2)设点B的平面PCD的距离为d,利用VB﹣PCD=VP﹣BCD即可得出.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知集合A=[a﹣3,a],函数 ![]() (﹣2≤x≤5)的单调减区间为集合B.
(﹣2≤x≤5)的单调减区间为集合B.
(1)若a=0,求(RA)∪(RB);
(2)若A∩B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位要在800名员工中抽去80名员工调查职工身体健康状况,其中青年员工400名,中年员工300名,老年员工100名,下列说法错误的是( )
A.老年人应作为重点调查对象,故抽取的老年人应超过40名
B.每个人被抽到的概率相同为 ![]()
C.应使用分层抽样抽取样本调查
D.抽出的样本能在一定程度上反映总体的健康状况
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,D,E分别是BC,A1B1的中点. 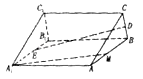
(1)求证:DE∥平面ACC1A1;
(2)设M为AB上一点,且AM= ![]() AB,若直三棱柱ABC﹣A1B1C1的所有棱长均相等,求直线DE与直线A1M所成角的正切值.
AB,若直三棱柱ABC﹣A1B1C1的所有棱长均相等,求直线DE与直线A1M所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,平面内有三个向量 ![]() ,
, ![]() ,
, ![]() ,其中
,其中 ![]() 与
与 ![]() 的夹角为30°,
的夹角为30°, ![]() 与
与 ![]() 的夹角为90°,且|
的夹角为90°,且| ![]() |=2,|
|=2,| ![]() |=2,|
|=2,| ![]() |=2
|=2 ![]() ,若
,若 ![]() =λ
=λ ![]() +μ
+μ ![]() ,(λ,μ∈R)则( )
,(λ,μ∈R)则( ) 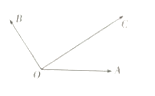
A.λ=4,μ=2
B.λ=4,μ=1
C.λ=2,μ=1
D.λ=2,μ=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={a|一次函数y=(4a﹣1)x+b在R上是增函数},集合B= ![]() .
.
(1)求集合A,B;
(2)设集合 ![]() ,求函数f(x)=x﹣
,求函数f(x)=x﹣ ![]() 在A∩C上的值域.
在A∩C上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com