
【题目】在直三棱柱ABC﹣A1B1C1中,D,E分别是BC,A1B1的中点. 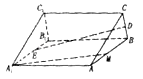
(1)求证:DE∥平面ACC1A1;
(2)设M为AB上一点,且AM= ![]() AB,若直三棱柱ABC﹣A1B1C1的所有棱长均相等,求直线DE与直线A1M所成角的正切值.
AB,若直三棱柱ABC﹣A1B1C1的所有棱长均相等,求直线DE与直线A1M所成角的正切值.
【答案】
(1)证明:取AB中点N,连结EN,DN,
∵在△ABC中,N为AB中点,D为BC中点,
∴DN∥AC,
∵DN平面ACC1A1,AC平面ACC1A1,
∴DN∥平面ACC1A1,
∵在矩形ABB1A1中,N为AB中点,E为A1B1中点,
∴EN∥平面ACC1A1,
又DN平面DEN,EN平面DEN,
DN∩EN=N,∴平面DEN∥平面ACC1A1,
∵DE平面DEN,∴DE∥平面ACC1A1.
(2)解:作DP⊥AB于P,
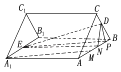
∵直三棱柱ABC﹣A1B1C1的所有棱长均相等,D为BC的中点,
∴DP⊥平面ABB1A1的所有棱长相等,D为BC的中点,
∴DP⊥平面ABB1A1,且PB= ![]() AB,又AM=
AB,又AM= ![]() AB,
AB,
∴MP= ![]() AB,
AB,
∵A1E=EP,A1M=EP,
∴∠DEP是直线DE与直线A1M所成角,
∴由DP⊥平面ABB1A1,EP平面ABB1A1,得DP⊥EP,
设直线三棱柱ABC﹣A1B1C1的棱长为a,
则在Rt△DPE中,DP= ![]() ,EP=A1M=
,EP=A1M= ![]() a,
a,
∴tan∠DEP= ![]() =
= ![]() .
.
∴直线DE与直线A1M所成角的正切值为 ![]() .
.
【解析】(1)取AB中点N,连结EN,DN,则DN∥AC,从而DN∥平面ACC1A1,再求出EN∥平面ACC1A1,从而平面DEN∥平面ACC1A1,由此能证明DE∥平面ACC1A1.(2)作DP⊥AB于P,推导出∠DEP是直线DE与直线A1M所成角,由此能求出直线DE与直线A1M所成角的正切值.
【考点精析】掌握直线与平面平行的判定和空间角的异面直线所成的角是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则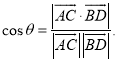 .
.


科目:高中数学 来源: 题型:
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长 ![]() 米.
米. 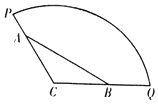
(1)当∠BAC=45°时,求观光道BC段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中A、B两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①过异面直线a,b外一点P有且只有一个平面与a,b都平行;
②异面直线a,b在平面α内的射影相互垂直,则a⊥b;
③底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
④直线a,b分别在平面α,β内,且a⊥b,则α⊥β.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果实数x,y满足(x﹣2)2+y2=2,则 ![]() 的范围是( )
的范围是( )
A.(﹣1,1)
B.[﹣1,1]
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣∞,﹣1]∪[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有6道题,其中3道甲类题,2道乙类题,张同学从中任取2道题解答.试求: (Ⅰ)所取的2道题都是甲类题的概率;
(Ⅱ)所取的2道题不是同一类题的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC与平面ABCD所成角为45° 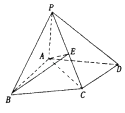
(1)若E为PC的中点,求证:PD⊥平面ABE;
(2)若CD= ![]() ,求点B到平面PCD的距离.
,求点B到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC. (Ⅰ)求证:OE⊥FC:
(Ⅱ)若 ![]() =
= ![]() 时,求二面角F﹣CE﹣B的余弦值.
时,求二面角F﹣CE﹣B的余弦值.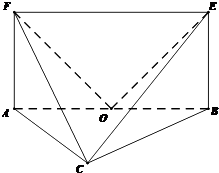
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,只需把函数y=sin2x的图象上所有的点( )
)的图象,只需把函数y=sin2x的图象上所有的点( )
A.向左平行移动 ![]() 个单位长度
个单位长度
B.向右平行移动 ![]() 个单位长度
个单位长度
C.向左平行移动 ![]() 个单位长度
个单位长度
D.向右平行移动 ![]() 个单位长度
个单位长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com