
【题目】如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC. (Ⅰ)求证:OE⊥FC:
(Ⅱ)若 ![]() =
= ![]() 时,求二面角F﹣CE﹣B的余弦值.
时,求二面角F﹣CE﹣B的余弦值.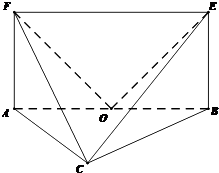
【答案】证明:(Ⅰ)连结OC,∵AC=BC,O是AB的中点, 故OC⊥AB.
又∵平面ABC⊥平面ABEF,
故OC⊥平面ABE,于是OC⊥OF.
又OF⊥EC,∵OF⊥平面OEC,
∴OF⊥OE,
又∵OC⊥OE,∴OE⊥平面OFC,
∴OE⊥FC;
(Ⅱ)解:由(I)得AB=2AF.不妨设AF=1,AB=2,
∵ ![]() =
= ![]() ,∴AC=
,∴AC= ![]() ,则OC=
,则OC= ![]()
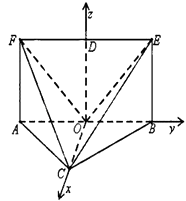
建立以O为坐标原点,OC,OB,OD分别为x,y,z轴的空间直角坐标系如图:
则F(0,﹣1,1),E(0,1,1),B(0,1,0),C( ![]() ,0,0),则
,0,0),则![]() =(﹣
=(﹣ ![]() ,1,1),
,1,1), ![]() =(0,﹣2,0),
=(0,﹣2,0),
设平面FCE的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 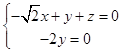 .
.
∴ ![]() =(1,0,
=(1,0, ![]() ),
),
∵ ![]() =(0,0,1),
=(0,0,1), ![]() =(
=( ![]() ,﹣1,0),
,﹣1,0),
∴同理可得平面CEB的法向量为 ![]() =(1,
=(1, ![]() ,0),
,0),
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
∵二面角F﹣CE﹣B是钝二面角,
∴二面角F﹣CE﹣B的余弦值为﹣ ![]() .
.
【解析】(Ⅰ)连结OC,则OC⊥AB,从而得到OC⊥OF,进而得到OF⊥OE,由此能证明OE⊥FC. (Ⅱ)由(I)得AB=2AF.不妨设AF=1,AB=2建立空间坐标系,求出平面的法向量,利用向量法即可.
【考点精析】利用直线与平面垂直的性质对题目进行判断即可得到答案,需要熟知垂直于同一个平面的两条直线平行.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】已知点P(2,0)及圆C:x2+y2﹣6x+4y+4=0.
(1)设过P直线l1与圆C交于M、N两点,当|MN|=4时,求以MN为直径的圆Q的方程;
(2)设直线ax﹣y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,D,E分别是BC,A1B1的中点. 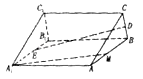
(1)求证:DE∥平面ACC1A1;
(2)设M为AB上一点,且AM= ![]() AB,若直三棱柱ABC﹣A1B1C1的所有棱长均相等,求直线DE与直线A1M所成角的正切值.
AB,若直三棱柱ABC﹣A1B1C1的所有棱长均相等,求直线DE与直线A1M所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王、小李两位同学玩掷骰子(骰子质地均匀)游戏,规则:小王先掷一枚骰子,向上的点数记为x;小李后掷一枚骰子,向上的点数记为y.
(1)求x+y能被3整除的概率;
(2)规定:若x+y≥10,则小王赢,若x+y≤4,则小李赢,其他情况不分输赢.试问这个游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为 ![]() ,圆心在直线l1:x﹣y+1=0上的圆C与直线l2:
,圆心在直线l1:x﹣y+1=0上的圆C与直线l2: ![]() x﹣y+1﹣
x﹣y+1﹣ ![]() =0相交于M,N两点,且|MN|=
=0相交于M,N两点,且|MN|= ![]()
(1)求圆C的标准方程;
(2)当圆心C的横、纵坐标均为整数时,若对任意m∈R,直线l3:mx﹣y+ ![]() +1=0与圆C恒有公共点,求实数a的取值范围.
+1=0与圆C恒有公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣3x﹣10<0},B={x|m+1≤x≤2m﹣1}.
(1)当m=3时,求集合(UA)∩B;
(2)若A∩B=B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足(x﹣a)(x﹣3a)<0,其中a>0,命题q:实数x满足 ![]() .
.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com