
【题目】已知点P(2,0)及圆C:x2+y2﹣6x+4y+4=0.
(1)设过P直线l1与圆C交于M、N两点,当|MN|=4时,求以MN为直径的圆Q的方程;
(2)设直线ax﹣y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
【答案】
(1)解:由于圆C:x2+y2﹣6x+4y+4=0的圆心C(3,﹣2),半径为3,
|CP|= ![]() ,而弦心距d=
,而弦心距d= ![]() ,
,
所以d=|CP|= ![]() ,所以P为MN的中点,
,所以P为MN的中点,
所以所求圆的圆心坐标为(2,0),半径为 ![]() |MN|=2,
|MN|=2,
故以MN为直径的圆Q的方程为(x﹣2)2+y2=4
(2)解:把直线ax﹣y+1=0即y=ax+1.代入圆C的方程,消去y,整理得(a2+1)x2+6(a﹣1)x+9=0.
由于直线ax﹣y+1=0交圆C于A,B两点,
故△=36(a﹣1)2﹣36(a2+1)>0,即﹣2a>0,解得a<0.
则实数a的取值范围是(﹣∞,0).
设符合条件的实数a存在,
由于l2垂直平分弦AB,故圆心C(3,﹣2)必在l2上.
所以l2的斜率kPC=﹣2,
∴kAB=a= ![]() ,
,
由于 ![]() ,
,
故不存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB
【解析】(1)由利用两点间的距离公式求出圆心C到P的距离,再根据弦长|MN|的一半及半径,利用勾股定理求出弦心距d,发现|CP|与d相等,所以得到P为MN的中点,所以以MN为直径的圆的圆心坐标即为P的坐标,半径为|MN|的一半,根据圆心和半径写出圆的方程即可;(2)把已知直线的方程代入到圆的方程中消去y得到关于x的一元二次方程,因为直线与圆有两个交点,所以得到△>0,列出关于a的不等式,求出不等式的解集即可得到a的取值范围,利用反证法证明:假设符合条件的a存在,由直线l2垂直平分弦AB得到圆心必在直线l2上,根据P与C的坐标即可求出l2的斜率,然后根据两直线垂直时斜率的乘积为﹣1,即可求出直线ax﹣y+1=0的斜率,进而求出a的值,经过判断求出a的值不在求出的范围中,所以假设错误,故这样的a不存在.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】等比数列![]() 中,
中, ![]() 分别是下表中第
分别是下表中第![]() 行中的某一个数,且
行中的某一个数,且![]() 中任何两个数不在下表的同一列中.
中任何两个数不在下表的同一列中.
第 | 第 | 第 | |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A=[a﹣3,a],函数 ![]() (﹣2≤x≤5)的单调减区间为集合B.
(﹣2≤x≤5)的单调减区间为集合B.
(1)若a=0,求(RA)∪(RB);
(2)若A∩B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8 cm,AB=10 cm,点P由C出发以每秒2 cm的速度沿线段CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2 s时,⊙O的半径是( )
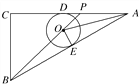
A. ![]() cm B.
cm B. ![]() cm C.
cm C. ![]() cm D. 2 cm
cm D. 2 cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,我国南海某处的一个圆形海域上有四个小岛,小岛B与小岛A、小岛C相距都为5n mile,与小岛D相距为 ![]() n mile.小岛A对小岛B与D的视角为钝角,且
n mile.小岛A对小岛B与D的视角为钝角,且 ![]() .
.
(Ⅰ)求小岛A与小岛D之间的距离和四个小岛所形成的四边形的面积;
(Ⅱ)记小岛D对小岛B与C的视角为α,小岛B对小岛C与D的视角为β,求sin(2α+β)的值.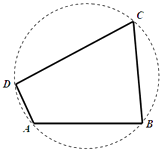
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔1小时抽一包产品,称其重量(单位:克)是否合格,分别做记录,抽查数据如下:
甲车间:102,101,99,98,103,98,99;
乙车间:110,115,90,85,75,115,110.
(1)问:这种抽样是何种抽样方法;
(2)估计甲、乙两车间包装产品的质量的均值与方差,并说明哪个均值的代表性好,哪个车间包装产品的质量较稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一块大型的广告宣传版面,其形状如图所示的直角梯形![]() .某厂家因产品宣传的需要,拟出资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形
.某厂家因产品宣传的需要,拟出资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形![]() (点
(点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() 在线段
在线段![]() 上).已知
上).已知![]() ,
,![]() ,其中曲线段
,其中曲线段![]() 是以
是以![]() 为顶点,
为顶点,![]() 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.

(1)求线段![]() ,线段
,线段![]() ,曲线段
,曲线段![]() 所围成区域的面积;
所围成区域的面积;
(2)求厂家广告区域![]() 的最大面积.
的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com