
【题目】现有一块大型的广告宣传版面,其形状如图所示的直角梯形![]() .某厂家因产品宣传的需要,拟出资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形
.某厂家因产品宣传的需要,拟出资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形![]() (点
(点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() 在线段
在线段![]() 上).已知
上).已知![]() ,
,![]() ,其中曲线段
,其中曲线段![]() 是以
是以![]() 为顶点,
为顶点,![]() 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.

(1)求线段![]() ,线段
,线段![]() ,曲线段
,曲线段![]() 所围成区域的面积;
所围成区域的面积;
(2)求厂家广告区域![]() 的最大面积.
的最大面积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知点P(2,0)及圆C:x2+y2﹣6x+4y+4=0.
(1)设过P直线l1与圆C交于M、N两点,当|MN|=4时,求以MN为直径的圆Q的方程;
(2)设直线ax﹣y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且sinA+![]() cosA=2.
cosA=2.
(Ⅰ)求角A的大小;
(Ⅱ)现给出三个条件:①a=2;②B=45°;③c= ![]() .试从中选出两个可以确△ABC的条件,写出你的选择,并以此为依据求△ABC的面积.(只写出一个方案即可)
.试从中选出两个可以确△ABC的条件,写出你的选择,并以此为依据求△ABC的面积.(只写出一个方案即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一批材料可以建成80m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的小矩形(如图所示),且围墙厚度不计,则围成的矩形的最大面积为( ) 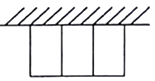
A.200m2
B.360m2
C.400m2
D.480m2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2x+2 ![]() sinxsin(x+
sinxsin(x+ ![]() )(ω>0).
)(ω>0).
(1)求f(x)的最小正周期;
(2)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ< ![]() )的图象与y轴的交点为(0,
)的图象与y轴的交点为(0, ![]() ),它的一个对称中心是M(
),它的一个对称中心是M( ![]() ,0),点M与最近的一条对称轴的距离是
,0),点M与最近的一条对称轴的距离是 ![]() .
.
(1)求此函数的解析式;
(2)求此函数取得最大值时x的取值集合;
(3)当x∈(0,π)时,求此函数的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC是边长为1的正三角形,点P1 , P2 , P3四等分线段BC(如图所示).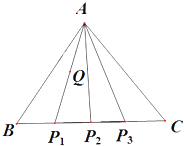
(1)求 ![]()
![]() +
+ ![]()
![]() 的值;
的值;
(2)Q为线段AP1上一点,若 ![]() =m
=m ![]() +
+ ![]()
![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“斐波那契数列”是数学史上一个著名数列,在斐波那契数列{an}中,a1=1,a2=1,an+2=an+1+an(n∈N*)则a8=;若a2018=m2+1,则数列{an}的前2016项和是 . (用m表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com